
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶9.3 동적 프로그래밍 (Dynamic Programming
9.3.2 가치 반복 알고리즘
동적 프로그래밍은 부트스트랩(bootstrap) 방식
- 모든 상태가 부정확한 값으로 출발하여 이웃 상태와 정보를 주고받으며 점점 수렴해 가는 방식
- ex. FrozenLake에서는 목적지에 인접한 상태부터 정확해져서 점점 멀리 확산
- 부트스트랩 : agent가 자체적으로 가치 함수나 q-value 함수를 업데이트하는 것
- 당장의 보상과 이웃 상태에서의 가치 함숫값이나 q-value 함숫값을 이용
- 이웃 상태(neighbor state)는 어떤 상태에서 가능한 바로 다음 상태들을 의미
동적 프로그래밍의 한계
- 마르코프 결정 프로세스를 알아야만 적용 가능하다.
- s, a, r에 대한 정보 필요하다.
- 크기가 작은 문제에 국한하여 적용 가능하다.(표를 사용하기 때문)
- 상태 공간과 행동 공간의 크기가 커지면 필요한 계산량이 기하급수적으로 증가한다.
- 차원의 저주(curse of dimensionality)
- 연속적인 상태와 행동 공간을 가지는 문제를 해결할 수 없다.
▶9.4 학습 기반 알고리즘
훈련 데이터를 활용한 '학습' 기반 알고리즘
- 동적 프로그래밍은 상태 전이 확률을 완벽히 알아야만 적용 가능하다.
- 상태 전이 확률이 없는 경우, 환경을 시뮬레이션하여 데이터, 즉 에피소드를 수집한다.
- ex. 프로 기사가 둔 바둑 기보 또는 프로그램과 프로그램을 대결시키는 셀프 플레이로 데이터를 수집한다.
- 초기 버전 알파고 한정
- 알파고 제로는 기보를 이용하지 않는다.
9.4.1 몬테카를로 방법
에피소드에서 데이터를 수집
- 에피소드의 표현
- e = [s0, a0, r0],..., [st, at, rt], [st+1, at+1, rt+1],..., [sT]
- ex. FrozenLake에서 수집한 에피소드
- e1 = [0, 1, 0], [4, 2, 0], [5] (사망)
- e2 = [0, 2, 0], [1, 2, 0], [2, 2, 0], [3, 0, 0], [2, 1, 0], [6, 1, 0], [10, 1, 0], [14, 2, 1], [15] (골인)
- 상태를 중심으로 에피소드를 잘라 데이터를 수집한다.

데이터를 가지고 가치 함수를 계산하는 몬테카를로 방법

- Z(2) = {([2,2,0], [3,0,0], [2,1,0], [6,1,0], [10,1,0], [14,2,1], [15]), ([2,1,0], [6,1,0], [10,1,0], [14,2,1], [15])}
- Z(2,1) = {([2,1,0], [6,1,0], [10,1,0], [14,2,1], [15] }
- 몬테카를로 방법은 데이터를 활용하기 때문에 학습 기반인데,
- 이웃 상태의 정보를 고려하지 않기 때문에 부트스트랩이 아니다.
- 각 에피소드 전체의 결과를 이용한다.
- 동적 프로그래밍은 데이터를 활용하지 않기 때문에 학습 기반이 아닌데,
- 이웃 상태를 고려하므로 부트스트랩 방식이다.
- 모든 state를 해야 한다. 룰이 없어서 어렵다.
- 학습 방법과 부트스트랩의 장점을 결합하여 더 좋은 알고리즘을 만들 수 있을까?
9.4.2 시간차 학습 알고리즘 : Sarsa와 Q러닝
시간차 학습(time-difference(TD) learning(의 핵심 아이디어
- 식 (9.14)에서는 Z에 있는 모든 샘플이 종료 순간 T까지 도달해야 함.

- 종료 순간까지 가봐야 누적 보상액을 알 수 있기 때문
- 종료 순간까지 가보지 않고 단지 이웃 상태로 전환하여 가치 함수를 개선할 수는 없나?
시간차 학습을 위한 공식 유도
- e = [s0, a0, r0],..., [st, at, rt], [st+1, at+1, rt+1],..., [sT]로부터
- t 순간에 추출한 샘플 z = [st, at, rt], [st+1, at+1, rt+1],..., [sT]를 처리한다고 가정하고
- 식 (9.14)를 다시 쓰면,

- z가 k번째 추가된다면, (vold : k-1개 샘플에서의 가치함수, vnew : k개 샘플에서의 가치함수)

- 위 첨자를 제거(vold가 vnew로 수렴)하고 1/k를 p로 대치하면,
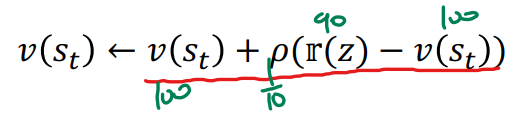

- 시간차 학습
- 식 (9.16’)과 식 (9.17’)은 에피소드를 사용하므로 학습 기반이고 st와 st+1이 같이 등장하므로 부트스트랩 방식이다.
- 학습 기반의 장점과 부트스트랩의 장점을 결합한 혁신적인 알고리즘
- Sarsa와 Q 러닝의 두 가지 알고리즘이 있다.
Sarsa
- 04, 06, 07행이 s-a-r-s’-a’ 고리를 만들고, 08행은 sarsa 고리를 식 (9.17)에 대입하여 가치 함수를 개선한다.
- st, at, rt, st+1, at+1
- 켜진 정책(on-policy) 방식 (결정을 내리는 데 사용되는 정책을 평가하거나 개선)
- 07행에서 현재 가치 함수 q에 의존
- Policy를 따르는 행동을 통해 q-value function 업데이트

Q 러닝
- 가치 함수 q에 의존하는 대신 max 연산자를 사용한다.

- 꺼진 정책(off-policy) 방식 (데이터를 생성하는 데 사용된 정책과 다른 정책을 평가하 거나 개선)
- 주어진 policy와 다른 행동을 취한다.

- SARSA는 정책을 따라 행동을 취하고, q-function을 update 한다.
- Q 러닝은 정책을 따르지 않고 취할 수 있는 가장 greedy 한 다음 행동을 했을 때의 q-function 값을 update 한다.
- 그래도 실제로 다음 행동을 취할 때는 현재 정책을 따른다.
9.4.3 Q 러닝 프로그래밍
FrozonLake에 Q 러닝 적용한 코드와 탐욕 적용한 코드 보기
참조표 방식의 한계
- 상태 가치 함수를 표현하는 v 또는 행동 가치 함수를 표현하는 q는 각각 1차원 과 2차원 배열.
- 이것을 사용하는 알고리즘을 참조표(lookup table) 방식이라 부름 §
- 상태의 개수가 방대한 경우 참조표 방식은 비현실적임
- ex. 바둑 3361 ≒ 1.74*10^172개의 상태
▶9.5 DQN
참조표 없이 가치 함수를 계산하는 방법은?
- 신경망이 대안이다.
- 신경망은 입력과 출력을 연결해 주는 일종의 함수이므로 가치 함수를 표현할 수 있다.
- 가장 중요한 문제는 학습에 사용할 훈련 집합을 수집하는 방법을 찾는 것이다.
- 강화 학습에서 '특징 벡터-레이블'의 샘플 수집이 가능한가?
- 레이블은 누가 어떻게 달아주나?
- 딥마인드는 에피소드에서 샘플을 추출하고 레이블을 자동으로 달아주는 획기적인 알고리즘 개발*.
- 비디오 게임에 적용하여 사람 수준의 프로그램을 만들었다.
9.5.1 DQN의 원리
DQN
- 딥러닝과 Q 러닝을 결합하여 뛰어난 성능을 달성하는 신경망 모델
- [그림 5 -8]의 깊은 다층 퍼셉트론 또는 [그림 6 -10]의 컨볼루션 신경망에 Q 러닝이 사용하는 식 (9.18)을 결합
가치 함수를 추정해 주는 신경 망([그림 9-10(a)]
- 입력은 상태 s이고 출력은 가치 함수의 값 q(s, a )
- 최적의 신경망이 있다면 모든 게임을 이길 수 있다.
- 상태 s에 서 q(s, a)를 계산하고 가장 큰 q값을 만드는 a를 선택하면 된다.
- 어떻게 이런 신경망을 만들까?

훈련 집합 수집 방법
- Q 러닝에서 생성되는 에피소드로부터 샘플을 수집
- 에피소드에서 t 순간은 [st, at, rt] [st+1, at+1]
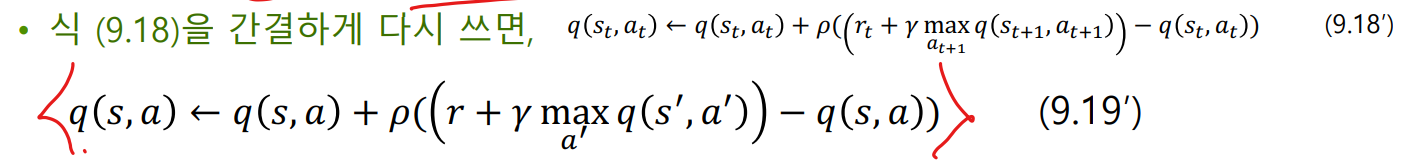
- [그림 9-11]은 신경망 입장에서 식 (9.19’)를 해석
- 현재 q(s, a)를 신경망의 추정치, 식 (9.19)의 오른쪽 변을 레이블로 간주
- q(s, 0), q(s, 1) 값을 추정 (0: 왼쪽으로 이동, 1: 오른쪽으로 이동)
- s : 수레의 상태

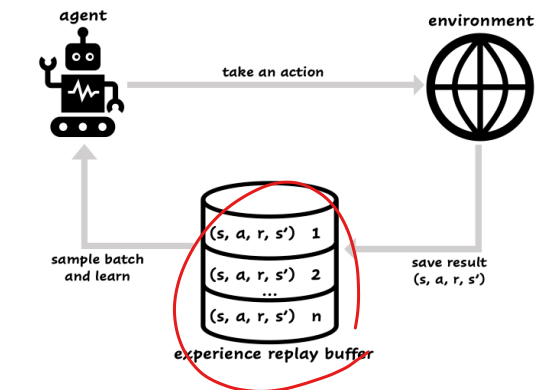
리플레이 메모리
- 샘플 간의 상관관계가 높은 문제
- t가 1에서 2로, 2에서 3으로, 3에서 4로 … 바뀔 때 샘플을 수집하여 샘플 간의 유사도 증가
- 리플레이 메모리로 해결
- 추출한 샘플로 바로 학습하는 대신 리플레이 메모리에 저장해 둔다.
- 실제 학습은 리플레이 메모리에서 랜덤 하게 샘플을 추출하여 미니배치를 구성하여 수행한다.
- 리플레이 메모리가 꽉 차면 가장 오래된 것을 삭제하고 추가 → 큐로 구현한다.
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능] 10장. 생성 모델(Generative Model) 2 (0) | 2023.06.05 |
|---|---|
| [인공지능] 10장. 생성 모델(Generative Model) 1 (0) | 2023.06.04 |
| [인공지능] 9장. 강화 학습(Reinforcement Learning) 2 (0) | 2023.05.30 |
| [인공지능] 9장. 강화 학습(Reinforcement Learning) 1 (0) | 2023.05.30 |
| [인공지능] 8장. 시계열 데이터와 순환 신경망4 (1) | 2023.05.24 |