
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
컴퓨터로 이런 방식의 학습을 할 수 있을까?
- 지금까지 공부한 지도 학습(다층 퍼셉트론, 컨볼루션 신경망, 순환 신경망)은 부적절하다.
- 입력/환경 정보를 한 번에 또는 순차적으로 넣고 결과를 확인하는 방법이다.
- 중간에 입력/환경 정보가 바뀌지는 않는다. (은닉층은 바뀔 수 있다.)
- 대안이 필요하다.
강화 학습(Reinforcement Learning)
- Reinforcement : 보상과 처벌을 통해 행동을 형성하는 과정 (심리학/행동)
- 보상 또는 페널티와 같은 피드백으로 에이전트의 학습 과정을 돕는 방법이다.
(Use feedback in the form of rewards or penalties to guide the learning process of an agent)
- 에이전트: 환경과 상호작용하며 정해진 목적을 이루기 위해 행동하는 인공지능 시스템
▶9.1 강화 학습의 원리와 응
강화 학습의 성공 사례
- 이세돌을 이긴 AlphaGo (DeepMind)
- OG를 이긴 OpenAI Five
- 로봇이나 자율 주행차 제어 등
9.1.0 탐사형 정책과 탐험형 정책
정책(policy)
- 에이전트가 주어진 상태(State)에서 어떤 행동(Action)을 선택할지 결정하는 규칙이나 전략이다.
탐사형 정책(exploitation policy)
- 이미 알려진 영역이나 분야를 더 자세히 조사하고 연구하는 과정이다.
- 아는 한도에서 최고의 결과를 야기하는 행동을 취하는 것이다.
- ex. 몇 번 시도해 보고 이후에는 그때까지 승률이 가장 높은 손잡이만 당기는 극단적인 탐사형 정책
탐험형 정책(exploration policy)
- 미지의 영역이나 분야를 발견하고, 조사하며 이해하는 과정이다.
- 지금까지 해보지 않았지만, 더 좋은 결과를 야기할 수도 있는 행동을 취하는 것이다.
- ex. 처음부터 끝까지 무작위로 선택하는 극단적인 탐험형 정책
탐사형 정책 vs 탐험형 정책 비교 예제
- 가장 좋아하는 식당 가기 vs 새로운 식당 찾아보기
- 가장 유명한 영화 보기 vs 무작위로 영화 골라 보기
탐험과 탐사 사이의 균형을 잘 맞추는 것이 중요하다.
- 너무 많은 탐험은 에이전트가 시간을 낭비한다.
- 너무 많은 탐사는 에이전트가 최적의 해를 놓칠 수 있다.
- 그 중간 어디
- 초기에는 탐험을 많이 하다가, 학습이 진행되면서 점차 탐사를 더 많이 하는 방향
탐험은 어렵다.
- 보통 탐험해야 하는 곳이 너무 많아 탐험할 수 있는 최적의 방법 필요하다.
- 다중 손잡이 밴딧 문제은 가장 간단한 예제이다.
에피소드(episode)
- 강화 학습에서는 게임을 시작하여 마칠 때까지 기록을 에피소드라 부른다.
9.1.1 다중 손잡이 밴딧 문제
multi-armed bandit 문제
- $1을 넣고 여러 손잡이 중 하나를 골라 당기면 $1을 잃거나 딴다.
- 손잡이마다 승률이 정해져 있는데 사용자는 확률을 모른다. ( p(r = 1 | 손잡이i) )
- 행동의 집합 : A = {a1, a2,..., an} {손잡이1, 손잡이2,..., 손잡이n}
- 보상의 집합 : {-1, 1}
- r(action = 손잡이i) ~ p(r | 손잡이i)
- r(ai)~p∂i(ri)
- p(ri = 1) = ∂i, p(ri = -1) = 1 - ∂i
- 탐험으로 확률을 찾고 탐사로 돈을 벌어야 한다.
- 행동 → 상태 변화 → 보상의 학습 사이클에서 상태가 없는 단순한 문제
- 행동 → 보상 사이클, 행동에 따른 상태 변화가 없다.
- 보상이 최근 취한 행동에만 관련이 있기 때문이다.
랜덤 정책을 쓰는 알고리즘
import numpy as np
# 다중 손잡이 밴딧 문제 설정
arms_profit=[0.4, 0.12, 0.52, 0.6, 0.25]
n_arms=len(arms_profit)
n_trial=10000 # 손잡이를 당기는 횟수(에피소드 길이)
# 손잡이 당기는 행위를 시뮬레이션하는 함수(handle은 손잡이 번호)
def pull_bandit(handle):
q=np.random.random()
if q<arms_profit[handle]:
return 1
else:
return -1
# 랜덤 정책을 모방하는 함수
def random_exploration():
episode=[]
num=np.zeros(n_arms) # 손잡이별로 당긴 횟수
wins=np.zeros(n_arms) # 손잡이별로 승리 횟수
for i in range(n_trial):
h=np.random.randint(0,n_arms)
reward=pull_bandit(h)
episode.append([h,reward])
num[h]+=1
wins[h]+=1 if reward==1 else 0
return episode, (num,wins)
e,r=random_exploration()
print("손잡이별 승리 확률:", ["%6.4f"% (r[1][i]/r[0][i]) if r[0][i]>0 else 0.0 for i in range(n_arms)])
print("손잡이별 수익($):",["%d"% (2*r[1][i]-r[0][i]) for i in range(n_arms)])
print("순 수익($):",sum(np.asarray(e)[:,1]))
ε-탐욕 알고리즘
- 탐욕 알고리즘(greedy algorithm)
- 과거와 미래를 전혀 고려하지 않고 현재 순간의 정보만 가지고 현재 최고 유리한 선택을 하는 알고리즘 방법론
- 탐사형에 치우친 알고리즘
- ε-탐욕 알고리즘은 기본적으로 탐욕 알고리즘인데, ε 비율만큼 탐험을 적용하여 탐사와 탐험의 균형을 추구
ε-탐욕 알고리즘
# ε-탐욕을 구현하는 함수
def epsilon_greedy(eps):
episode=[]
num=np.zeros(n_arms) # 손잡이별로 당긴 횟수
wins=np.zeros(n_arms) # 손잡이별로 승리 횟수
for i in range(n_trial):
r=np.random.random()
if(r<eps or sum(wins)==0): # 확률 eps로 임의 선택
h=np.random.randint(0,n_arms)
else:
prob=np.asarray([wins[i]/num[i] if num[i]>0 else 0.0 for i in range(n_arms)])
prob=prob/sum(prob)
h=np.random.choice(range(n_arms),p=prob)
reward=pull_bandit(h)
episode.append([h,reward])
num[h]+=1
wins[h]+=1 if reward==1 else 0
return episode, (num,wins)
e,r=epsilon_greedy(0.1)
print("손잡이별 승리 확률:", ["%6.4f"% (r[1][i]/r[0][i]) if r[0][i]>0 else 0.0 for i in range(n_arms)])
print("손잡이별 수익($):",["%d"% (2*r[1][i]-r[0][i]) for i in range(n_arms)])
print("순 수익($):",sum(np.asarray(e)[:,1]))이때까지 추정한 확률에 따라 손잡이 선택하는 부분
→ h=np.random.choice(range(n_arms), p=prob)
- 하지만 추정 확률에 따라 손잡이를 선택하는 건 최고 유리한 선택이 아니라고 하셨다.
- 기댓값이 가장 높은 손잡이를 선택하는 게 최고 유리한 선택!!
→ h=np.argmax(prob)를 사용하는 게 더 좋다고 하셨다.
몬테카를로 방법
- 현실 세계의 현상 또는 수학적 현상을 난수를 생성해 확률적 시뮬레이션하는 기법
- 복잡한 문제나 고차원적인 문제에서 정확한 해답을 찾기 어려울 때 사용한다.
- 무작위 표본(random samples)을 추출하고 이러한 표본들의 평균을 계산하여 근삿값을 계산한다.
- random_exploration 함수와 epsilon_greedy 함수는 몬테카를로 방법이다.
- 인공지능은 다양한 목적으로 몬테카를로 방법 활용한다.
9.1.2 OpenAI의 gym 라이브러리
gym 라이브러리 (https://gym.openai.com)
- OpenAI 재단이 만들어 배포하는 라이브러리로서 여러 강화 학습 문제를 제공한다.
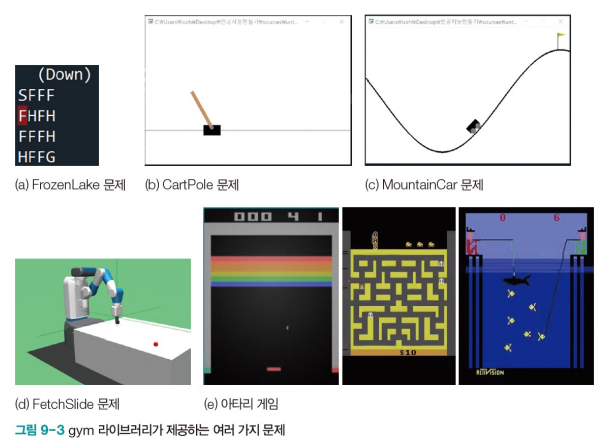
FrozenLake 문제
- 단순하지만 강화학습의 개념을 설명하는데 유익한 문제이다.
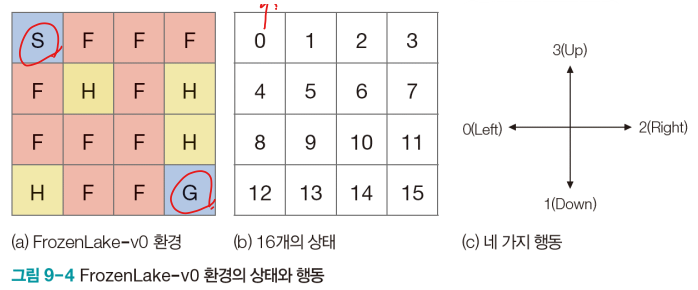
- S에서 시작하여 G에 도착하면 이기는 게임이다.
- F는 얼어 있어 밟고 지날 수 있으나 H는 구멍이라 빠지면 진다.
- H와 F는 감추어져 있다.
- 현재 있는 곳이 상태 {0,1,…,15}, 좌우상하 이동이 행동 {Left, Down, Right, Up}
- 6개의 상태를 벗어날 수는 없다.
- 0에서 Up 또는 Left 행동하면 그대로 0에 있다. (count는 1 추가된다.)
FrozenLake-v1
import gym
# 환경 불러오기
env=gym.make("FrozenLake-v1",is_slippery=False, render_mode='human')
print(env.observation_space)
print(env.action_space)
n_trial=20
# 에피소드 수집
env.reset()
episode=[]
for i in range(n_trial):
action=env.action_space.sample() # 행동을 취함(랜덤 선택)
obs,reward,done,truncated, info=env.step(action) # 보상을 받고 상태가 바뀜
episode.append([action,reward,obs])
env.render()
if done or truncated:
break
print(episode)
env.close()
9.1.3 계산 모형
마르코프 결정 프로세스(MDP Markov decision process)
- 상태의 종류, 행동의 종류, 보상의 종류를 지정한다.
- 행동을 취했을 때 발생하는 상태 변환을 지배하는 규칙을 정의한다.

상태와 환경, 보상
- 상태 집합 : S = {s1, s2,..., sl}
- 행동 집합 : A = {a1, a2,..., am}
- 보상 집합 : R = {r1, r2,..., rn}
보상이 주어지는 시점
- 즉시 보상
- ex. 다중 손잡이 밴딧
- 지연된 보상
- ex. FrozenLake, 바둑, 장기, 비디오 게임
상태 전이
- 결정론적 환경 (100% 확률로 새로운 상태가 정해지는 환경)
- ex. FrozenLake 문제에서 Right를 선택하면 100% 확률로 오른쪽으로 이동한다.
- P(s' = 2, r = 0 | s = 1, a = 2) = 1.0
- 상태 1(s=1)에서 행동 2(a=2)를 취하면
- 새로운 상태 2(s'=2)로 전환하고 보상이 0(r=0) 일 확률이 1
- 스토캐스틱 환경 (확률 분포에 따라 새로운 상태가 다르게 정해지는 환경)
- is_slippery를 True로 설정하면 스토케스틱 환경이 된다.
- Right를 선택해도 일정한 확률로 오른쪽으로 이동하지 않을 수 있다.
- 실제 세계에서 발생하는 바람 또는 얼음 위의 미끄러짐을 흉내 낸다.
- 바둑이나 장기, 비디오 게임 등은 모두 결정론적 환경
▶9.2
9.2.1 강화 학습과 지도 학습의 비교
| 지도 학습(신경망) | 강화 학습 | |
| 문제(데이터) | 훈련 집합 X(특징 벡터)와 Y(레이블) | 환경 또는 환경에서 수집한 데이터 |
| 최적화 목표 | 신경망 출력 o와 레이블 y의 오차인 || o - y || 최소화 |
누적 보상 최대화 |
| 학습 알고리즘이 알아내야 하는 것 | 오차를 최소화하는 신경망의 가중치 | 누적 보상을 최대화하는 최적 정책 |
| 품질을 평가하는 함수 | 손실 함수 | 가치 함수 |
| 학습 알고리즘 | 스토케스틱 그레이디언트 하강법 (SGD) |
동적 프로그래밍, Saras, Q 러닝, DQN 등 |
강화 학습
당장은 손해가 나더라도 전체 과정에 걸쳐 누적 보상액을 최대화해야 한다.
ex. 바둑에서 작은 집을 희생하여 최종적으로 더 많은 집을 확보
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능] 9장. 강화 학습(Reinforcement Learning) 3 (0) | 2023.06.04 |
|---|---|
| [인공지능] 9장. 강화 학습(Reinforcement Learning) 2 (0) | 2023.05.30 |
| [인공지능] 8장. 시계열 데이터와 순환 신경망4 (1) | 2023.05.24 |
| [인공지능] 8장. 시계열 데이터와 순환 신경망3 - LSTM 편곡 (1) | 2023.05.14 |
| [인공지능] 8장. 시계열 데이터와 순환 신경망2 - 비트코인 가격 예측 (3) | 2023.05.10 |