
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
그래프 이론 : Graph Theory
정점의 집합과 간선의 집합으로 구성된 그래프를 연구하는 수학의 한 분야
그래프 : 𝐺 = (𝑉, 𝐸)
- 𝑉 : 정점의 집합, 𝐸 : 간선의 집합

네트워크 과학: Network Science
다양한 학문 분야에 펼쳐져 있던 복잡계의 연구 대상들이
- '네트워크'라는 하나의 주제로 통일되면서 발생한 학제 간 연구 분야
복잡계 네트워크 : Complex Network
- 사회 현상의 탐구 : 소셜 네트워크 - 사람과 사람 사이의 관계 분석
- 생명 현상의 탐구 : 단백질 네트워크 - 분자와 분자 사이의 관계 분석
- 자연 현상의 탐구 : 상전이 현상 – 네트워크 동역학으로 분석 가능
작은 세상 네트워크 : Small-World Network
6단계의 분리: 세상이 참 좁은 이유에 대한 과학적 설명
소수의 원거리 연결만으로도 전체 네트워크의 평균 거리가 크게 짧아진다.

척도 없는 네트워크 : Scale-Free Network
빈익빈 부익부 : 네트워크에서 허브가 생겨나는 이유에 대한 과학적 설명
선호적 연결에 의해 평균 이상으로 많은 링크를 가진 허브가 탄생한다.
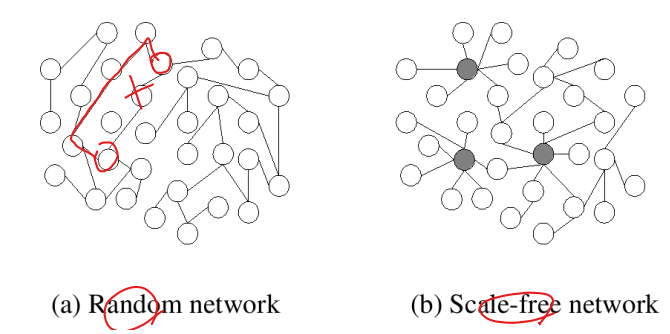
네트워크 분석 : Network Analysis
자연과학, 생명과학, 사회과학 등 모든 분야를 아우르는 데이터 과학 분야
- 소셜 네트워크 분석 : SNA, Social Network Analysis
- 복잡계 네트워크 분석 : Complex Network Analysis
주요 탐구 주제
- 중심성 분석 : Centrality Analysis
- 군집 분석: Cluster Analysis
네트워크 분석을 위한 기본 용어
방향 그래프, 무방향 그래프 : directed and undirected
가중치 그래프, 가중치 없는 그래프 : weighted and unweighted
인접 행렬, 인접 리스트 : adjacency matrix and list
단순 경로, 경로 길이, 랜덤 워크 : simple path, path length, random walk
네트워크 분석을 위한 기본 정보
노드(정점)와 연결(간선)의 수 : Number of nodes and edges
평균 차수 : Average degree
밀도, 반경, 반지름 : Density, Diameter, Radius
평균 최단거리 : Average shortest path length
강연결/약연결 컴포넌트
- Number of Strongly Connected Components (SCC)
- Number of Weakly Connected Components (WCC)
중심성 분석 : Centrality Analysis
네트워크에서 중심부에 위치한 (가장 중요한) 노드를 찾기 위한 방법
- 예) 인스타그램에서 10대 남성에게 가장 영향력이 높은 인플루언서는?
중심성 지수 : Centrality Measures
- 차수 중심성 : Degree Centrality
• 한 노드에 연결된 모든 연결의 개수로 중심성을 평가하는 지수
- 𝐶𝑑(𝑣𝑖) = 𝑑𝑖
• 방향 그래프에서는 in-degree와 out-degree로 구분
- 인접 중심성 : Closeness Centrality
• 한 노드가 다른 노드들로 가는 최단 경로가 얼마나 짧은 지를 평가
• 가정 : 다른 모든 노드들로 가는 경로가 짧을수록 중심성이 높을 것이다.
- 평균 최단 경로 길이가 짧은 노드일수록 중심성이 높다.
- 매개 중심성 : Betweenness Centraliity
• 한 노드가 네트워크의 다른 노드 간의 연결에 얼마나 기여하는 지를 평가
- 페이지랭크 : PageRank
• 고유벡터 중심성 : Eigenvector Centrality
• Katz 중심성 : 고유벡터 중심성을 방향 그래프에 적용
• 페이지랭크 중심성
- 핵인싸와 친구인 노드가 모두 인싸라고 할 수 있을까?
- 특정 노드의 영향력은 그 노드의 차수에 반비례해서 전파되어야 한다.
네트워크에서의 유사도 척도 : Similarity Measures
그래프 내부의 인접한 두 정점 간의 유사도를 측정하려면?
- 두 노드의 이웃이 얼마나 겹치는 지를 평가
- 𝜎(𝑣𝑖 , 𝑣𝑗) = |𝑁(𝑣𝑖) ∩ 𝑁(𝑣𝑗)|
- 𝑁(𝑣𝑖): 노드 𝑣𝑖의 이웃 노드들의 집합
유사도 척도의 정규화 : Normalization
유사도 척도를 [0, 1] 구간의 값으로 정규화하는 방법
자카드 유사도 : Jaccard Similarity
- 𝜎Jaccard(𝑣𝑖, 𝑣𝑗) = |𝑁(𝑣𝑖) ∩ 𝑁(𝑣𝑗)| / |𝑁(𝑣𝑖) ∪ 𝑁(𝑣𝑗)|
코사인 유사도 : Cosine Similarity
- 𝜎Cosine(𝑣𝑖, 𝑣𝑗) = |𝑁(𝑣𝑖) ∩ 𝑁(𝑣𝑗)| / root(|𝑁(𝑣𝑖)| × |𝑁(𝑣𝑗)|)
네트워크의 군집도
전이적 연결: Transitive Linking
- 유유상종 : 내 친구의 친구는 내 친구일 가능성이 높다.
- (𝑣𝑖 , 𝑣𝑗) ⋀(𝑣𝑗 , 𝑣𝑘) → (𝑣𝑖 , 𝑣𝑘)
군집 계수 : Clustering Coefficient
- 노드들이 얼마나 서로 똘똘 뭉쳐 있는가를 평가
커뮤니티 분석 : Community Analysis
군집. vs. 커뮤니티 : Cluster. vs. Community
- 본질적으로는 같은 의미이나, 목적과 수단이 서로 다른 배경에서 출발
- 군집 : 특성에 의해 나누어진 군집을 발견하는 것이 목적 (IRIS)
- 커뮤니티 : 나누어진 군집을 발견해서 특성을 이해하는 것이 목적 (SNS)
커뮤니티 발견 : Community Detection
- 네트워크의 연결 구조를 이용한 클러스터링 알고리즘
- 때로는 고정된 커뮤니티가 아닌, 진화하는 커뮤니티 발견이 문제일 수 있다.
커뮤니티 구조의 평가
지도 학습
- 실제로 해당 노드가 어떤 커뮤니티에 속하는 지를 아는 경우
- 혼동 행렬을 통한 평가 지표를 사용할 수 있음
★비지도 학습
- 해당 노드가 어떤 커뮤니티에 속하는 지를 모르는 경우
- 커뮤니티의 구조가 네트워크의 구조를 얼마나 잘 반영했는가를 평가
모듈성 : Modularity
기본 아이디어 : 커뮤니티 구조는 랜덤 네트워크의 구조와는 달라야 한다.
가중치 없는 무방향 그래프 𝐺 = (𝑉, 𝐸)에서,
- 전체 간선의 수가 |𝐸| = 𝑚이라면,
- 차수가 𝑑𝑖 , 𝑑𝑗인 두 노드 𝑣𝑖 , 𝑣𝑗 가 서로 연결되어 있을 확률은 얼마인가?
뉴먼 모듈성 지수 : Newman’s Modularity
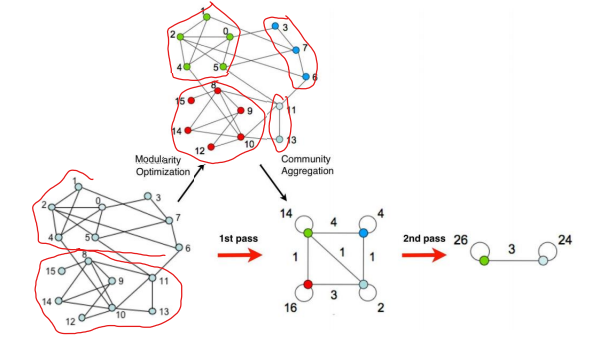
루베인 알고리즘 : Louvain Method
뉴먼의 모듈성 지수를 최적화하는 알고리즘
1단계 : 한 노드를 현재 커뮤니티에서 빼내어 인접한 커뮤니티에 재배치
- 모듈성 지수가 증가하면 해당 커뮤니티에 배치, 아니면 원래 커뮤니티에 둔다.
2단계 : 1단계에서 생성된 커뮤니티를 하나의 노드로 하는 그래프를 새로 만든다.
- 커뮤니티의 내부 링크는 self-loop의 가중치로,
- 커뮤니티 간 연결은 해당 커뮤니티 간의 연결 가중치의 합으로 결정한다.
위와 같은 pass(1단계+2단계)를 모듈성 지수 증가가 없을 때까지 반복
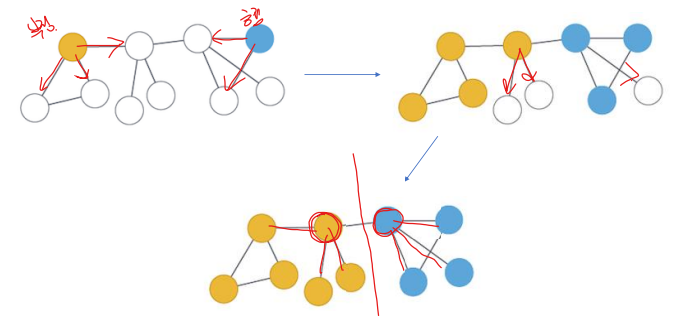
라벨 전파 알고리즘 : LPA, Label Propagation Algorithm
가정 : 내가 속한 커뮤니티는 내 이웃들이 많이 속해 있는 커뮤니티와 같다.
각자가 가진 라벨을 네트워크에 전파하여 마지막에 남은 라벨로 커뮤니티 결정한다.
LABEL-PROPAGATION-ALGORITHM
- 모든 노드가 각자의 고유한 라벨을 소유한다.
- 임의의 순서로 각 노드는 이웃 노드들이 가장 많이 가진 라벨로 업데이트한다.
- 모든 노드의 라벨이 이웃 노드들 중 가장 많은 라벨로 구성되면 종료한다.
- 이웃 노드의 라벨의 개수가 동일하면 임의로 하나 선정한다.
'컴퓨터공학 > 데이터과학기초' 카테고리의 다른 글
| [데이터과학기초] 텍스트 분석 (0) | 2023.01.10 |
|---|---|
| [데이터과학기초] 인공신경망 (0) | 2023.01.10 |
| [데이터과학기초] 군집 분석 (Clustering) (2) | 2023.01.09 |
| [데이터과학기초] 로지스틱 회귀와 분류 (0) | 2023.01.02 |
| [데이터과학기초] 선형 회귀와 예측 (0) | 2022.12.30 |