
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
선형모델의 일반화
선형회귀분석을 위한 조건
- 결과변수가 연속형 변수이면서 정규분포를 따라야 한다.
선형회귀분석을 위한 조건에 맞지 않는 경우
- 결과변수가 범주형 변수일 때 : 로지스틱 회귀분석
- 결과변수가 어떤 사건이 발생하는 횟수일 때 : 포아송 회귀분석
일반화 선형모델 : generalized linear model
선형회귀모델을 확장 : 정규분포를 따르지 않는 결과변수에 대한 회귀모델 생성
- 표준 선형회귀모델 : μy = b0 + b1x1 + b2x2 +... + bmxm
- - μy : 결과변수의 조건부 평균, xm : 예측변수, bm : 회귀계수, m : 변수의 개수
- 일반 선형회귀모델 : f(μy) = b0 + b1x1 +... + bmxm
- - f(μy) : 결과변수의 조건부 평균의 함수(link function)
표준 선형회귀모델은 일반선형모델의 한 특수한 경우
- 링크함수가 항등함수 : (μy) = μy
- 확률분포는 정규분포를 따른다.
회귀계수의 추정 : 최대우도법(MLE, Maximum Likelihood Estimation)
로지스틱 회귀분석 : logistic regression analysis
- 결과변수가 범주형 변수일 때 : 정규분포를 따르지 않는다.
- 이중 변수(binary variable) : 예/아니요, 성공/실패, 생존/사망 등
- 다중 변수(multicategory variable) : 우수/보통/미흡, A/B/AB/O 등
포아송 회귀분석 : Poisson regression analysis
- 결과변수가 어떤 사건이 발생하는 횟수일 때 : 포아송 분포를 따른다.
- 연관 철도사고 횟수, 월간 빈집털이 횟수, 일간 상담 횟수 등
- 횟수변수는 포아송 분포를 따르고, 평균과 분산은 종종 상관관계를 가진다.
이항 로지스틱 회귀분석 : binomial logistic regression analysis
결과변수가 이분형 범주일 때 특정 사건이 발생할 확률을 직접 추정
- 결과변수의 예측값이 항상 1, 0 사이의 확률 값
- 확률값이 0.5보다 크면 사건 발생, 작으면 발생하지 않는다.
- ex. 기업부도가 발생할 확률
로지스틱 변환 : logistic transformation
- 예측변수의 선형결합을 로그 변환한 결과변수로 나타낸다.
이항 로지스틱 회귀모델 : binomial logistic regression model
- ln(p / (1 - p)) = b0 + b1x1 +... + bmxm
- p : 이항 사건의 성공 확률(사건발생), 1 - p : 이항 사건의 실패 확률(미발생)
오즈 : odds
- odds = p / (1 - p) : 사건 발생확률 대 사건 미발생 확률의 비율
- 로짓(logit) : 오즈에 로그를 취한 값 = ln(p / (1 - p))
로지스틱 회귀모델
- 로그오즈(log odds = logit)에 대한 이항분포
- 링크함수가 로그오즈이며 확률분포는 이항분포
- 사건발생확률 p에 대해서 정리
- p(사건발생) = e^z / (1 + e^z) = 1 / (1 + e^-z), z = b0 + b1x1 +... + bmxm
- 회귀계수를 알면 결과변수의 사건발생확률을 구할 수 있다.
예측 : prediction
- 새로운 예측변수의 값을 입력하면 결과 변숫값이 1인 확률을 예측할 수 있다.
- 훈련 데이터로부터 회귀계수를 학습한 결과로 시험 데이터의 고객이 이탈할 확률을 예측할 수 있다.
분류와 군집화 : Classification vs Clustering
분류 : 지도학습 (정답이 있는 데이터 셋을 분류하는 것)
- ex. iris 데이터셋에서 품종의 분류
- ex. titanic 데이터셋에서 생존 여부를 예측
군집화 : 비지도학습 (정답이 없는 데이터셋을 분류하는 것)
- ex. iris 데이터셋에서 모양이 유사한 꽃들의 군집 찾기
- ex. titanic 데이터셋에서 서로 가까운 사람들의 군집 찾기
분류기의 종류
- 로지스틱 회귀분석(logistic regression)
- 의사결정 트리(decision tree)
- 랜덤 포리스트(random forest)
- k-최근접 이웃(kNN, k-nearest-neighbor)
- 나이브 베이지안(naive bayesian)
- 서포트 벡터 머신(SVM, support vector machine)
이진분류 : binary classification
- 분류도 예측의 일종이지만, 종속변수가 범주형 변수
- 이진분류 : 종속변수 값의 범위가 두 개일 때
- ex. titanic 데이터셋 : survival 변수(생존, 사망)는 둘 중의 하나
- ex. 암 진단: 종속 변수가 암에 (걸렸거나, 걸리지 않았거나) 둘 중의 하나
로지스틱 : logistic
로지스틱 회귀 : Logistic Regression
- 종속변수의 값이 바이너리 형태인 경우에 적용하기 좋은 회귀 분석 모델
- 직선으로는 이런 데이터를 잘 설명할 수 없으므로, 적절한 곡선을 찾아야 한다.
로지스틱 함수: Logistic Function
- 바이너리 값을 가지는 범주형 데이터를 잘 설명해 주는 지수 함수
- y = 1 / (1 + e^-x) , e는 자연상수(오일러의 수, 네이피어의 수)
로지스틱 함수의 성질과 활용
- 시그모이드 함수: Sigmoid Function
- bounded : 유한한 구간 (a, b) 사이의 한정된 값을 갖는다.
- monotonic: 항상 양의 기울기를 가지는 단조증가함수다.
로지스틱 함수를 분류의 기준을 충족할 확률로 해석
- 𝑦 = 𝛼𝑥 + 𝛽, 𝑓(𝑥) = 1 1+𝑒^−(𝛼𝑥+𝛽)
- 𝑓(𝑥) > 0.5 : 𝑦 = 1이라고 분류
- 𝑓(𝑥) < 0.5: 𝑦 = 0이라고 분류
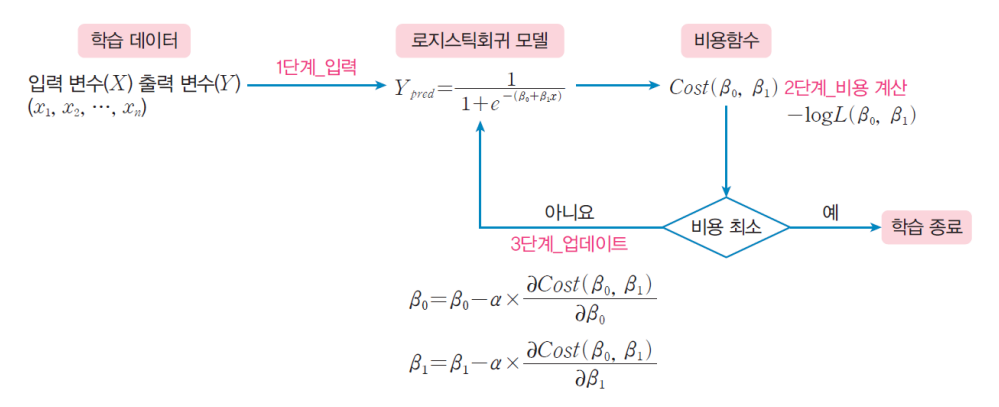
로지스틱 회귀식을 찾는 방법
- 로지스틱 함수 𝑓(𝑥)에서 가장 적절한 𝛼와 𝛽 찾기
- 최대우도추정법 : MLE, Maximum Likelihood Estimation
- 우도 함수: Likelihood Function
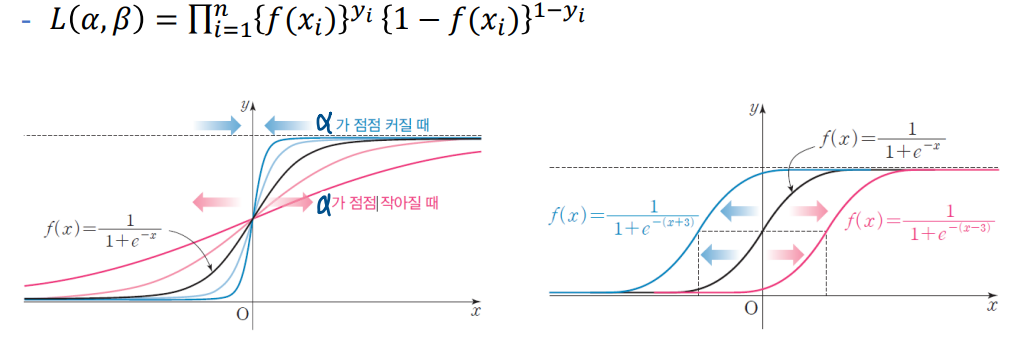
이진 분류의 결과 표현
혼동 행렬: Confusion Matrix
- 이진 분류기의 분류 결과를 2 × 2 행렬로 표시한 행렬
- 이진 분류기가 분류(예측)할 때, 얼마나 많이 헷갈렸는가를 나타낸다.
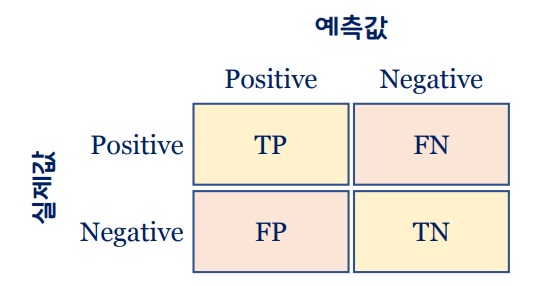
- type 1 error : FP
- type 2 error : FN
분류 모델의 성능 평가 지표 : Evaluation Metric
정확도 : CA, Classification Accuracy
- 𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦 = (𝑇𝑃 + 𝑇𝑁) / (𝑇𝑃 + 𝑇𝑁 + 𝐹𝑃 + 𝐹𝑁)
정밀도 : Precision
- 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 = 𝑇𝑃 / (𝑇𝑃 + 𝐹𝑃) , 분류기가 양성으로 판정한 것이 얼마나 정확한가?
재현율 : Recall
- 𝑅𝑒𝑐𝑎𝑙𝑙 = 𝑇𝑃 / (𝑇𝑃 + 𝐹𝑁) , 분류기가 양성으로 판정한 것의 비율은 얼마인가?
F1-Score
- 𝐹1 = (2 × 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 × 𝑟𝑒𝑐𝑎𝑙𝑙) / (𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑟𝑒𝑐𝑎𝑙𝑙) , 정밀도와 재현율의 조화평균
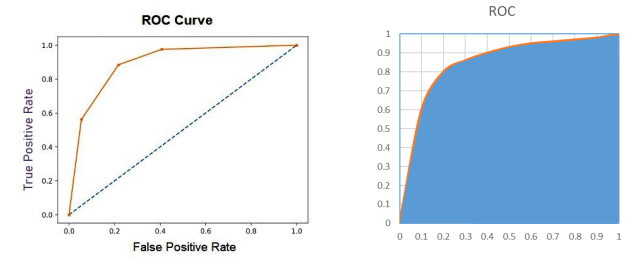
ROC 곡선 : Receiver Operation Characteristic Curve
- 이진 분류의 결과에서 FP 비율과 TP 비율의 관계를 그린 곡선
AUC : Area Under Curve
- ROC 곡선의 하부 면적으로 표현하는 성능 평가 지표
결정 트리 : Decision Tree
데이터를 학습해서 트리 기반의 분류 규칙을 만드는 방법
일종의 스무고개 방식: 분할 정복 (Divide-and-Conquer)
- 루트 노드 : 모든 데이터를 포함
- 중간 노드 : 특정 조건에 따른 데이터의 분할
- 리프 노드 : 분류 조건에 맞는 데이터의 집합
결정 트리를 학습하는 방법
- 분할 조건이 되는 특징을 어떻게 식별할 것인가?
- 순도(purity) : 단일 분류 데이터를 포함하는 정도
- 분류의 기준 : 각 단계별로 순도가 높아지는 방향으로 분류
정보 이득 : information gain
- 데이터를 나누기 전과 데이터를 나눈 후의 정보량의 변화
정보 엔트로피: Information Entropy
- 정보량 : 어떤 데이터가 포함하고 있는 정보의 총 기대치
- 어떤 사건이 발생할 확률이 𝑝이면 그 사건의 정보량은 log𝑏 (1/𝑝)
- 어떤 사건의 정보량의 기대치 : 𝑝 log𝑏 1 𝑝 = −𝑝 log𝑏 𝑝
정보 엔트로피 : 전체 사건의 기대치
- 각 사건의 기대치의 합
데이터의 순도가 높아지는 방향: 정보 엔트로피가 낮아지는 방향
'컴퓨터공학 > 데이터과학기초' 카테고리의 다른 글
| [데이터과학기초] 인공신경망 (0) | 2023.01.10 |
|---|---|
| [데이터과학기초] 군집 분석 (Clustering) (2) | 2023.01.09 |
| [데이터과학기초] 선형 회귀와 예측 (0) | 2022.12.30 |
| [데이터과학기초] 탐색적 데이터 분석 (1) | 2022.12.29 |
| [데이터과학기초] 데이터 과학2 (0) | 2022.12.29 |