
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
회귀 : regression
'회귀'의 사전적 의미 : 되돌아감
회귀라는 용어의 유래
- 프랜시스 골턴의 유전학 연구에서 유래
- 회귀의 법칙 : the law of regression
회귀분석과 선형회귀
회귀분석 : regression analysis
- 독립변수와 종속변수의 관계를 잘 설명하는 회귀식을 찾는 과정
선형회귀 : linear regression
- 독립변수와 종속변수의 관계가 선형일 때
- 선형 회귀식(직선의 방정식) : y = b + ax
- 선형 회귀식의 절편(intercept)과 기울기(slope)를 알면 독립변수와 종속변수의 관계를 설명, 예측할 수 있다.
선형 회귀모델 : linear regression model
회귀식 : y + b0 + b1x
잔차(residual) : 실제 데이터의 값(관측값)과 회귀식의 값(예측값)과의 차이
- ri = yi - y^, ri : 잔차, yi : 관측값, y^ : 예측값
선형 회귀의 유형
단순 선형회귀 : simple(univariate) linear regression
- 한 개의 독립변수와 종속변수 간의 단순한(1차) 선형 관계
- ex. 교육기간과 평균소득 사이의 선형관계
다중 선형회귀 : multiple(multivariate) linear regression
- 두 개 이상의 독립변수와 종속변수 간의 선형 관계 (종속변수에 영향을 미치는 독립변수가 여러 개)
- 다중 회귀식 : y = b0 + b1x1 + b2x2 +... + bnxn
- ex. incom ~ education + women + prestige
다항 선형회귀 : polynomial linear regression
- 종속변수와 한 개의 독립변수의 다항식으로 구성된 비선형 관계
- 다항 회귀식 : y = b0 + b1x^1 + b2x^2 +... + bnx^n
- ex. 교육기간이 증가하면 평균 소득도 증가하지만, 한계가 있다.
모형 적합 : fitting a model
데이터(관측값)를 가장 잘 설명하는 선형 회귀식은?
- 데이터 전체를 고려했을 때, 잔차가 가장 작은 직선의 방정식
평균절대오차 : MAE(mean absolute error)
- 잔차의 평균
평균제곱오차 : MSE(mean squared error)
- 잔차 제곱의 평균
제곱근 평균제곱오차 : RMSE(rooted mean squared error)
- root(MSE)
결정계수 : coefficient of determination
R^2 (R-squared) : 선형 회귀식의 설명력 지표
- (관측값 - 평균) 제곱의 평균 / (실제값 - 평균) 제곱의 평균
- R^2 = 0 : 독립변수와 종속변수 간의 선형 관계가 존재하지 않는다.
- R^2 = 1 : 독립변수와 종속변수 간의 완전한 선형 관계가 존재한다.
Adjusted R^2 : 다중 독립변수의 영향을 줄여준다.
- R^2는 독립변수의 개수가 증가하면 항상 값이 증가한다.
- 독립변수의 개수가 많아지면 페널티를 부과하여 설명력을 보정한다.
- 과적합(overfitting)에 대한 고려
선형회귀 모델을 적용하기 위한 전제 조건
선형성 : linearity
- 독립변수와 종속변수 간의 선형적 관계가 존재한다.
정규성 : normality
- 종속변수의 값들이 정규분포를 가진다.
등분산성 : homoscedasticity, homogeneity of variance
- 종속변수 값들의 분포는 모두 동일한 분산을 가진다.
★독립성 : independence
- 모든 독립변수의 관측값들은 서로 독립이다.
- Y ~ X1 + X2
페널티 회귀분석 : penalized regression analysis
너무 많은 독립변수를 갖는 모델에 페널티를 부과하여 간명한 회귀모델을 생성
- 모델의 성능에 크게 기여하지 못하는 변수의 영향력을 축소하거나 제거
- 제약화, 규제화 : regularization, 축소 : shirinkage
회귀식에 페널티항을 추가
- 잔차제곱합과 페널티항의 합이 최소가 되는 회귀계수를 추정
릿지 회귀분석 : ridge regression analysis
- 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수 크기를 0에 근접하도록 축소
- L2-norm 페널티항으로 회귀모델에 페널티를 부과
- L2-norm : 각 회귀계수의 제곱합
- 릿지 회귀모델 : 잔차의 제곱합과 L2-norm의 합을 최소화하는 회귀계수 추정
라소 회귀분석 : lasso regression analysis
- 모델의 설명력에 기여하지 못하는 독립변수의 회귀계수 크기를 0으로 만듦(해당 독립변수를 모델에서 제거)
- L1-norm 페널티항으로 회귀모델에 페널티를 부과
- L1-norm : 각 회귀계수의 절댓값의 합
- 라소 회귀모델: 잔차의 제곱합과 L1-norm의 합을 최소화하는 회귀계수 추정
일래스틱넷 회귀분석 : elasticnet regression analysis
- L1-norm과 L2-norm을 모두 이용하여 회귀모델에 페널티를 부과
- a : 모델의 혼합 정도를 통제하는 파라미터
- a = 0 : 순수한 릿지회귀모델
- a = 1 : 순수한 라소회귀모델
- 0 < a < 1 : 릿지회귀모델과 라소회귀모델의 혼합 정도를 통제
비용 함수 : Cost Function
실제값과 예측값의 차이를 측정하는 함수
- 손실 함수 : Loss Function
- 목적 함수 : Objective Function
회귀식의 비용 함수를 최소화하는 기울기와 절편을 찾자.
- 회귀식의 비용 함수: RSS, MAE, MSE, RMSE
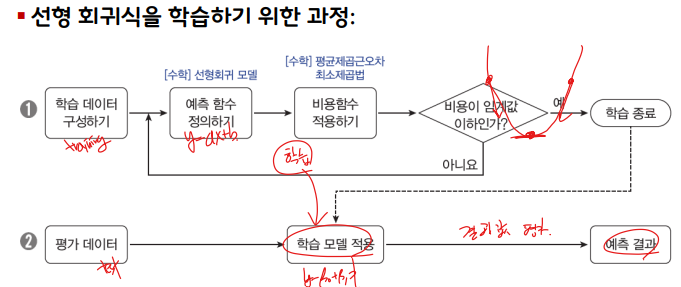
최소 제곱 추정법 : LSM, Least Square Method
선형 회귀식의 기울기와 절편을 찾는 가장 일반적인 방법
잔차 : residuals
- 𝑦의 실제값과 추정값 사이의 수직 거리의 차이 : r = y − y^
잔차 제곱합 : RSS, Residual Sum-of-Squares
- 잔차는 양수나 음수 모두 가능하므로 잔차의 제곱합을 구함
선형 회귀 분석의 목표
- 잔차 제곱합의 값이 최소가 되는 회귀식 찾기: y^ - ax^ + b
경사하강법: Gradient Descent
비용 함수(예: RSS)가 최소가 되는 기울기와 절편을 구하는 방법은?
- 반복적인 계산을 통해 점진적으로 하강하면서 파라미터를 추정함
더 나은 성능을 가진 학습 모델을 만들려면?
종속변수를 설명하는데 도움이 되는 독립변수가 여러 개일 때
- 모든 독립변수가 종속변수를 설명하는데 동일하게 기여하는가?
- 기여도가 높은 독립변수와 기여도가 낮은 독립변수를 구분
- 기여도가 낮거나 거의 없는 변수들은 학습 모형에서 제외시킴
설명변수의 숫자가 많을수록 좋은 학습 모델이라 할 수 있는가?
- 설명변수의 숫자가 적을수록 좋은 학습 모델이라 할 수 있
'컴퓨터공학 > 데이터과학기초' 카테고리의 다른 글
| [데이터과학기초] 군집 분석 (Clustering) (2) | 2023.01.09 |
|---|---|
| [데이터과학기초] 로지스틱 회귀와 분류 (0) | 2023.01.02 |
| [데이터과학기초] 탐색적 데이터 분석 (1) | 2022.12.29 |
| [데이터과학기초] 데이터 과학2 (0) | 2022.12.29 |
| [데이터과학기초] 데이터 과학 (0) | 2022.12.26 |