
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶5.5 깊은 다층 퍼셉트론
다층 퍼셉트론에 은닉층을 더 많이 추가하면 깊은 다층 퍼셉트론이다.
- 깊은 다층 퍼셉트론은 가장 쉽게 생각할 수 있는 딥러닝 모델이다.
- 그리고 은닉층 1개만 있어도 다층 퍼셉트론이다.
5.5.1 구조와 동작
깊은 다층 퍼셉트론(DMLP - deep MLP)의 구조
- L - 1개의 은닉층이 있는 L층 신경망이다.
- 입력층에 d + 1개의 노드, 출력층에 c개의 노드가 있다.
- i번째 은닉층에 ni개의 노드가 있다. (ni는 하이퍼 매개변수)
- 인접한 층은 완전 연결, 즉 FC(fully-connected) 구조이다.
- 아주 많은 가중치를 가진다.
- ex) ni = 500, L = 5라면,
MNIST데이터에서 (784 + 1) * 500 + (500 + 1) * 500 * 3 + (500 + 1) * 100 = 1,149,010개의 가중치
깊은 다층 퍼셉트론의 동작
- 아래 식은 l - 1번째 층과 l번째 층을 연결하는 가중치 행렬이다.

- 입력층으로 들어오는 특징 벡터


5.5.2 오류 역전파 알고리즘

5.5.3 깊은 다층 퍼셉트론 프로그래밍
깊은 다층 퍼셉트론으로 MNIST 인식
- 다층 퍼셉트론을 구현한 코드와 유사하다.
- 단지 은닉층 1개가 4개로 확장된 차이가 있다. (음영 부분만 달라진다.)
import numpy as np
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# MNIST 읽어 와서 신경망에 입력할 형태로 변환
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,784) # 텐서 모양 변환
x_test = x_test.reshape(10000,784)
x_train = x_train.astype(np.float32)/255.0 # ndarray로 변환
x_test = x_test.astype(np.float32)/255.0
y_train = tf.keras.utils.to_categorical(y_train,10) # 원핫 코드로 변환
y_test = tf.keras.utils.to_categorical(y_test,10)
n_input = 784
n_hidden1 = 1024
n_hidden2 = 512
n_hidden3 = 512
n_hidden4 = 512
n_output = 10
mlp=Sequential()
mlp.add (Dense(units=n_hidden1,activation='tanh', input_shape=(n_input,),
kernel_initializer='random_uniform', bias_initializer='zeros'))
mlp.add(Dense(units=n_hidden2,activation='tanh', kernel_initializer='random_uniform',
bias_initializer='zeros'))
mlp.add(Dense(units=n_hidden3,activation='tanh', kernel_initializer='random_uniform',
bias_initializer='zeros'))
mlp.add(Dense(units=n_hidden4,activation='tanh', kernel_initializer='random_uniform',
bias_initializer='zeros'))
mlp.add(Dense(units=n_output,activation='tanh', kernel_initializer='random_uniform',
bias_initializer='zeros'))
# 신경망 학습습
mlp.compile(loss='mean_squared_error',optimizer=Adam(learning_rate=0.001),metrics=['accuracy'])
hist = mlp.fit(x_train,y_train,batch_size=128,epochs=30,validation_data=(x_test,y_test),verbose=2)
# 신경망 정확률 측정정
res = mlp.evaluate(x_test,y_test,verbose=0)
print("정확률은",res[1]*100)5.5.4 가중치 초기화 방법
kernel_initializer='random_uniform'
- 균일 분포에서 난수를 생성해 가중치를 초기화한다.
Dense 함수의 API
- kernel_initializer의 기본값은 'glorot_uniform'이다.

- glorot_uniform은 [Glorot2010]에서 유래하는데, 텐서플로는 좋은 성능이 입증되었다 판단해 기본값으로 제공한다.
Xavier Glorot Initialization
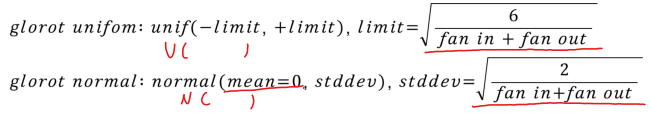
- fan-in : the maximum number of inputs that a system can accept.
- fan-out : the maximum number of inputs that the output of a system can feed to other systems.
- glorot_uniform 사용 시
- 성능 향상(tanh activation function과 같이 쓸 경우), 코드 간결하다.
mlp.add(Dense(units=n_hidden1, activation='tanh', input_shape=(n_input,)))
mlp.add(Dense(units=n_hidden2, activation='tanh'))
mlp.add(Dense(units=n_hidden3, activation='tanh'))
mlp.add(Dense(units=n_hidden4, activation='tanh'))
mlp.add(Dense(units=n_output, activation='tanh'))
Extra. 가중치 초기화를 잘해야 하는 이유 1
input Data 분포가 좋아도 layer를 통과하면 그 분포를 유지하기가 힘들다.
- 모든 activation 값이 0이 되거나, 1 or -1가 되거나 (tanh의 max가 1, min이 -1)
- (좌측) 초기 가중치 갑이 너무 적은 경우
- (우측) 초기 가중치 값이 너무 큰 경우
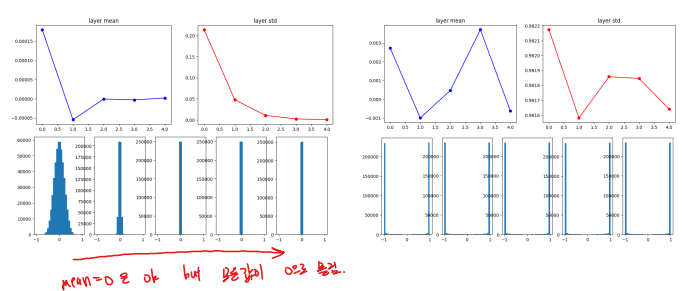
Extra. 가중치 초기화를 잘해야 하는 이유 2
Xavier Glorot Initialization 적용 시
- Glorot uniform

▶5.6 딥러닝의 학습 전략
층이 깊어지면 현실적인 문제 발생
- 그레이디언트 소멸 문제 (gradient diminish)
- 과잉 적합 문제 (overfitting)
5.6.1 그레이디언트 소멸 문제와 해결책
미분의 연쇄 법칙(chain rule)에 따르면,
- i번째 층의 그레이디언트는 오른쪽에 있는 i + 1번째 층의 그레이디언트에 자신 층에서 발생한 그레이디언트를 곱하여 구한다.
- 따라서 그레이디언트가 0.001처럼 적은 경우 왼쪽으로 진행하면서 점점 작아진다.
- 왼쪽으로 갈수록 가중치 갱신이 느려져서 전체 신경망의 학습이 매우 느린 현상이 발생한다.
ReLU 함수를 사용하여 해결
- tanh(s) 시그모이드 함수의 문제점
- s가 클 때 그레이디언트가 0에 가까워짐(s=8이면 그레이디언트 값은 0.0000004501)
-ReLU는 s가 음수일 때 그레이디언트는 0, 양수일 때 1

5.6.2 과잉 적합과 과잉 적합 회피 전략
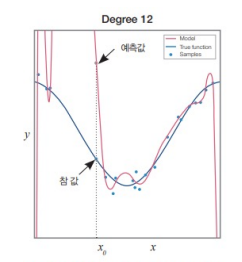
아래 그림은 과소 적합과 과잉 적합을 설명한다.
- x는 특징이고 y는 레이블인 회귀 문제로 설명
- 모델로 1차 다항식을 사용하면 과소 적합(under fitting, 데이터에 비해 모델 용량이 적은 상황)
- 용량이 가장 큰 12차 다항식은 훈련 집합에 대해 가장 적은 오류

과소 적합 - 주어진 학습 데이터도 못 맞춘다.
과잉 적합 - 학습 데이터에만 맞춰서 설계해 새로운 데이터가 들어오면 못 맞춘다.
12차 다항식 모델은 일반화 능력이 떨어진다.
- ex) x0에서 예측이 부정확하다.
- 데이터의 복잡도에 비해 너무 큰 용량의 모델을 사용한 탓 ← 과잉 적합(over fitting) 현상
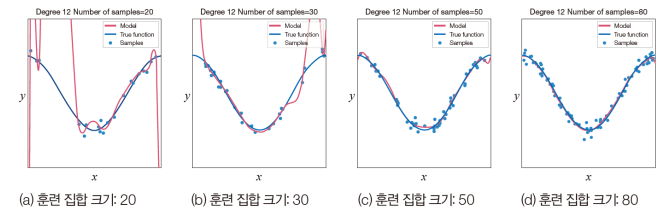
딥러닝의 과잉 적합 회피 전략
- 데이터 양을 늘린다.
- 데이터 양을 늘릴 수 없다면 훈련 샘플을 변형해 인위적으로 늘리는 데이터 증대(data augmentation)를 사용한다.
- 규제 기법 적용
- 데이터 증대, 가중치 감쇠, 드롭아웃, 앙상블 등
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능] 6장. 컨볼루션 신경망과 컴퓨터 비전1 (1) | 2023.04.13 |
|---|---|
| [인공지능] 5장. 딥러닝과 텐서플로3 (0) | 2023.04.12 |
| [인공지능] 5장. 딥러닝과 텐서플로1 (1) | 2023.04.10 |
| [인공지능] 4장. 신경망 기초3 (3) | 2023.04.06 |
| [인공지능] 4장. 신경망 기초2 (0) | 2023.04.06 |