
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶4.1 인공 신경망의 태동
인공 신경망은 생물 신경망에서 영감을 얻었지만 실제 구현은 다르다.
- 컴퓨터의 작동 원리가 생물의 작동원리와 근본적으로 다르기 때문이다.
4.1.1 생물 신경망
사람의 뇌와 컴퓨터
- 뉴런은 뇌의 정보처리 단위로서 연산을 수행하는 세포체이다.
- 처리한 정보를 다른 뉴런에 전달하는 축삭, 다른 뉴런으로부터 정보를 받는 수상돌기로 구성되어 있다.
- 사람 뇌는 10^11개가량의 뉴런, 뉴런마다 1000개가량의 연결이 있다. -> 고도의 병렬 처리기
- 반면에 폰 노이만 컴퓨터는 아주 빠른 순차 명령어 처리기이다.
▶4.2 퍼셉트론의 원리
퍼셉트론(perceptron)
- 현재 기준으로 매우 낡은 기술이지만 신경망 공부에서 중요하다.
- 퍼셉트론만 쓰는 경우 낡은 기술이라는 의미이다.
- 퍼셉트론은 다층 퍼셉트론과 딥러닝의 핵심 구성 요소이다.
- 퍼셉트론은 단순한 모델이라 기계 학습의 용어와 원리는 설명하는데 적합하다.
4.2.1 퍼셉트론의 구조와 연산
퍼셉트론의 구조
- 입력층과 출력층으로 구성되어 있다. (출력층은 한 개의 노드)
- 입력층은 d+1개의 노드 (d는 특징 벡터의 차원)
- iris는 d = 4, digit는 d = 64이다.
- 특징 벡터 : x = (x1, x2,..., xd)
- i번째 입력 노드와 출력 노드는 가중치 wi를 가진 엣지(edge)로 연결된다.
퍼셉트론의 연산
- i번째 엣지는 xi와 wi를 곱해 출력 노드로 전달한다.
- 0번째 입력 노드 x0은 1인 바이어스(bias) 노드이다.
- 출력 노드는 d+1개의 곱셈 결과를 모두 더한 s를 계산하고 활성함수(activation function)를 적용한다.

활성 함수
- 뉴런을 활성화하는 과정을 모방한다.
- 퍼셉트론은 활성 함수로 계단함수를 사용한다. (s가 0보다 크면 1, 그렇지 않으면 -1 출력)
- 퍼셉트론은 특징 벡터를 1 또는 -1로 변환하는 장치이다. (즉, 이진 분류기)

4.2.2 퍼셉트론으로 인식하기
퍼셉트론은 이진 분류기 (binary classifier)


4.2.3 행렬 표기
퍼셉트론의 동작을 행렬을 이용해 다시 쓰면,
- W와 X는 1 x d 행렬
- X의 전치(transpose) 행렬 X^T는 d x 1 행렬
- WX^T는 1 x 1 행렬로서 스칼라

- 보다 간결한 표현(바이어스를 첫 번째 요소로 추가)
- W를 1 × (d + 1) 행렬 (w0, w1, … , wd), X를 1 × (d + 1) 행렬 (x0, x1, … , xd)로 확장하면
– x0, w0는 어떤 값을 가지는가?
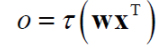
▶4.3 사람의 학습과 신경망의 학습
퍼셉트론의 학습
- 데이터와 함께 데이터를 인식하는 퍼셉트론(가중치)이 주어진다.
- 즉 데이터로 학습을 마친 퍼셉트론이 주어진다.
- 실제 상황에서는 데이터만 주어지므로, 학습 알고리즘으로 가중치(w0, w1, … , wd)를 알아내야 한다.
- OR 데이터의 경우 2차원 특징 벡터이고 샘플이 4개뿐이라 연필을 가지고 쉽게 가중치를 알아낼 수 있다.
- sklearn의 필기 숫자 데이터는 64차원 특징 벡터이고 1797개 샘플을 가지므로 학습 알고리즘 없이 불가능
▶4.4 퍼셉트론 학습 알고리즘



4.4.1 손실 함수 설계
손실 함수 J가 만족해야 할 조건
1. w가 훈련 집합에 있는 샘플을 모두 맞히면, 즉 정확률이 100%이면 J(w)는 0이다.
2. w가 틀리는 샘플이 많을수록 J(w)의 값이 크다.
조건을 만족하는 함수는 여러 개다.
- I는 W가 틀리는 샘플 X의 집합
- X가 +1 부류라면(즉 y = 1이라면), 퍼셉트론의 출력 WX^T는 음수, -y(WX^T)는 양수
- X가 -1 부류라면(즉 y = -1이라면), 퍼셉트론의 출력 WX^T는 양수, -y(WX^T)는 양수
- 결국 틀린 샘플 X는 손실 함수의 값을 증가시킨다.
- 틀린 샘플이 많을수록 손실 함숫값은 커진다.
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능] 5장. 딥러닝과 텐서플로1 (1) | 2023.04.10 |
|---|---|
| [인공지능] 4장. 신경망 기초3 (3) | 2023.04.06 |
| [인공지능] 4장. 신경망 기초2 (0) | 2023.04.06 |
| [인공지능] 3장. 기계 학습과 인식2 (0) | 2023.04.04 |
| [인공지능] 3장. 기계 학습과 인식1 (1) | 2023.04.04 |