
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶3.5 필기 숫자 인식
sklearn이 제공하는 fit 함수로 모델링(학습)한다.
predict 함수로 예측한다.
3.5.1 화소 값을 특징으로 사용
화소 각각을 특징으로 간주한다.
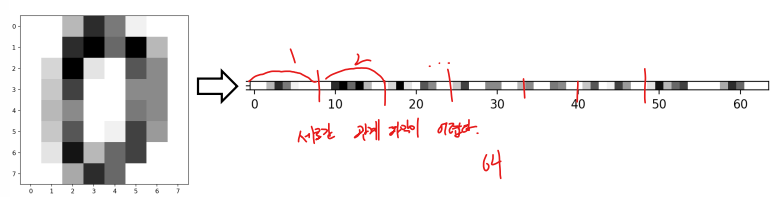
- sklearn의 필기 숫자는 8*8 맵으로 표현되므로 64차원 특징 벡터이다.
- 2차원 구조를 1차원 구조로 변환한다.
from sklearn import datasets
from sklearn import svm
digit = datasets.load_digits()
# svm의 분류기 모델 SC를 학습
s = svm.SVC(gamma=0.1, C=10)
# digit 데이터로 모델링
s.fit(digit.data, digit.target)
# 훈련 집합의 앞에 있는 샘플 3개를 새로운 샘플로 간주하고 인식해본다.
new_d = digit.data[0:3]
res = s.predict(new_d)
print('예측값은 ', res)
print('참값은 ', digit.target[0:3])
# 훈련 집합을 테스트 집합으로 간주하여 인식해보고 정확률을 측정
res = s.predict(digit.data)
correct = [i for i in range(len(res)) if res[i] == digit.target[i]]
accuracy = len(correct)/len(res)
print('화소 특징을 사용했을 때 정확률 = ', accuracy*100., '%')
▶3.6 성능 측정
객관적인 성능 측정의 중요성
- 모델 선택할 때 중요하다.
- 현장 설치 여부 결정할 때 중요하다.
일반화(generalization) 능력
- 학습(training set)에 사용하지 않았던 새로운 데이터(test set)에 대한 성능
- 가장 확실한 방법은 실제 현장에 설치하고 성능 측정 -> 비용 때문에 실제 적용이 어렵다.
- 주어진 데이터를 분할하여 사용하는 지혜 필요
- train, test 적당히 나누어야 한다.
- train set은 충분해야 하기에 보통 8대 2로 나눈다.
3.6.1 혼동 행렬과 성능 측정 기준
혼동 행렬(confusion matrix)
- 부류 별로 옳은 분류와 틀린 분류의 개수를 기록한 행렬
- nij는 모델이 i라고 예측했는데 실제 부류는 j인 샘플의 개수

- 이진 분류에서 긍정(positive)과 부정(negative)
- 검출하고자 하는 것이 긍정(환자가 긍정이고 정상인이 부정, 불량품이 긍정이고 정상이 부정)
- 참 긍정(TP), 거짓 부정(FN), 거짓 긍정(FP), 참 부정(TN)의 네 경우
- 뒤에 PN이 예측값, 앞에 TF는 예측의 True, False
널리 쓰이는 성능 측정 기준
정확률(accuracy)
- 부류가 불균형일 때 성능을 제대로 반영하지 못함
- 정확률 = 맞힌 샘플 수 / 전체 샘플수 = 대각선 샘플수 / 전체 샘플수
특이도(specificity)와 민감도(sensitivity) 의료에서 주로 사용
- 특이도 = TN / (TN + FP)
- 민감도 = TP / (TP + FN)
정밀도(precision)와 재현율(recall) 정보 검색에서 주로 사용
- 정밀도 = TP / (TP + FP) -> 긍정 예상 중에 진짜 긍정
- 재현율 = TP / (TP + FN) -> 실제 긍정 중에 긍정 예상

3.6.2 훈련/검증/테스트 집합으로 쪼개기
주어진 데이터를 적절한 비율로 훈련, 검증, 테스트 집합으로 나누어 쓴다.
- 모델 선택 포함 : 훈련/검증/테스트 집합으로 나눈다.
- 모델 선택 제외 : 훈련/테스트 집합으로 나눈다.

from sklearn import datasets, svm
from sklearn.model_selection import train_test_split
import numpy as np
# 데이터셋을 읽고 훈련 집합과 테스트 집합으로 분할
digit = datasets.load_digits()
# train 60%, test 40%로 랜덤 분할
x_train, x_test, y_train, y_test = train_test_split(digit.data, digit.target, train_size=0.6)
# svm의 분류 모델 SVC를 학습
s = svm.SVC(gamma=0.001)
s.fit(x_train, y_train)
res = s.predict(x_test)
#혼동 행렬 구하기
conf = np.zeros((10, 10))
for i in range(len(res)):
conf[res[i]][y_test[i]] += 1
for con in conf:
print(con)
# 정확률 측정하고 출력
num_correct = 0
for i in range(10):
num_correct += conf[i][i]
accuracy = num_correct / len(res)
print(accuracy * 100)
3.6.3 교차 검증
훈련/테스트 집합 나누기의 한계
- 우연히 높은 정확률 또는 우연히 낮은 정확률 발생 가능성이 있다.
k-겹 교차 검증 (k-fold cross validation)
- 훈련 집합을 k개의 부분 집합으로 나누어 사용한다.
- 한 개를 남겨두고 k-1개로 학습한 다음 남겨둔 것으로 성능을 측정한다.
- k개의 성능을 평균하여 신뢰도를 높인다.

from sklearn import datasets, svm
from sklearn.model_selection import cross_val_score
import numpy as np
digit = datasets.load_digits()
s = svm.SVC(gamma=0.001)
# 5-겹 교차 검증
accuracies = cross_val_score(s, digit.data, digit.target, cv=5)
print(accuracies)
print(accuracies.mean()*100, accuracies.std())- k를 크게 하면 신뢰도는 높아지지만 실행 시간이 더 걸린다.
▶3.7 인공지능은 어떻게 인식을 하나?
3.7.1 특징 공간을 분할하는 결정 경계
인공지능의 인식은 철저히 수학의 의존한다.
- 샘플은 특징 벡터로 표현되며, 특징 벡터는 특징 공간의 한 점에 해당한다.
- 인식 알고리즘은 원래 특징 공간을 성능을 높이는데 더 유리한 새로운 특징 공간으로 여러 차례 변환한다.
- 그다음 최종적으로 특징 공간을 분할하여 부류를 결정한다.
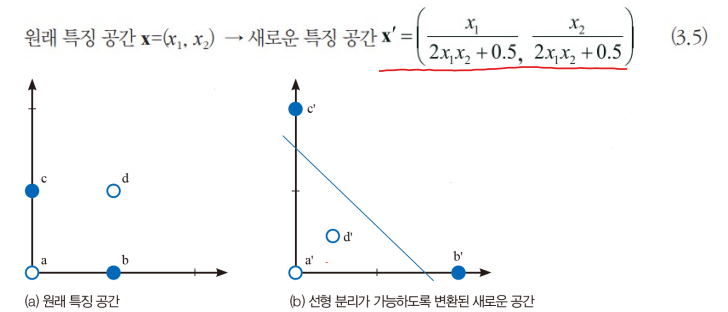
결정 경계를 정하는 문제에서 고려 사항
- 비선형 분류기(nonlinear classifier) 사용
- 과잉 적합(overfitting) 회피
- 과잉 적합은 아웃라이어를 맞히려고 과다하게 복잡한 결정 경계를 만드는 현상
- 훈련 집합에 대한 성능은 높지만 테스트 집합에 대해서는 형편없는 성능
3.7.2 SVM의 원리
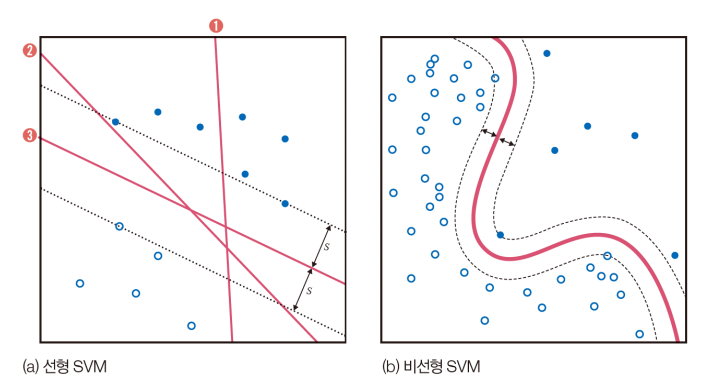
기계 학습의 목적은 일반화 능력을 극대화하는 것
- SVM은 일반화 능력을 높이려 여백을 최대화한다.
- 분류기 ②는 빨간색 부류에 조금만 변형이 생겨도 결정 경계를 넘을 가능성.
- ③은 두 부류 모두에 대해 멀리 떨어져 있어 경계를 넘을 가능성이 낮다.
- SVM은 두 부류까지의 거리인 2s를 여백(margin)이라 부른다.
- SVM 학습 알고리즘은 여백을 최대화하는 결정 경계를 찾는다.
SVM을 비선형 분류기로 확장
- 원래 SVM은 선형 분류기(a)
- 커널 트릭을 사용하여 비선형 분류기로 확장(커널 함수를 사용해 선형 공간을 비선형 공간으로 변형(b))
- 커널 함수로는 polynomial function, radial basis function, sigmoid 함수를 사용한다.
- 커널 함수의 종류와 커널 함수의 모양을 조절하는 매개변수는 하이퍼 매개변수
C라는 하이퍼 매개변수
- 지금까지 모든 샘플을 옳게 분류하는 경우를 다룬다.
- 실제로는 오류를 허용하는 수밖에 없다.
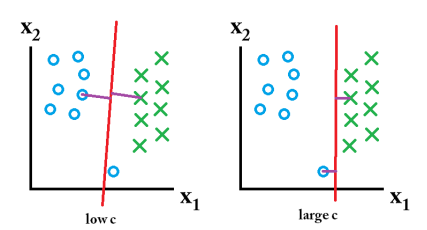
- C를 크게 하면, 잘못 분류한 훈련 집합의 샘플을 적은데 여백이 작아진다.
(훈련 집합에 대한 정확률은 높지만 일반화 능력 떨어진다.)
- C를 작게 하면, 여백은 큰데 잘못 분류한 샘플이 많아진다.
(훈련 집합에 대한 정확률은 낮지 만 일반화 능력 높아진다.)
'컴퓨터공학 > 인공지능' 카테고리의 다른 글
| [인공지능] 5장. 딥러닝과 텐서플로1 (1) | 2023.04.10 |
|---|---|
| [인공지능] 4장. 신경망 기초3 (3) | 2023.04.06 |
| [인공지능] 4장. 신경망 기초2 (0) | 2023.04.06 |
| [인공지능] 4장. 신경망 기초1 (1) | 2023.04.05 |
| [인공지능] 3장. 기계 학습과 인식1 (1) | 2023.04.04 |