
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
13장에서 one-dimentional search는 롤러코스터와 같았다.
two-dimensional의 경우, 산과 계곡의 이미지가 된다.
미분 평가를 필요로 하지 않는 접근법을 nongradient 방법 또는 direct 방법이라고 한다.
도함수를 필요로 하는 것들을 경사법(gradient) 또는 하강법(또는 상승법)이라고 한다.

▶Random Search
brute force 접근의 간단한 예는 random search method이다.
독립 변수의 랜덤하게 선택된 값에서 함수를 반복적으로 평가한다.
충분한 수의 샘플이 수행되면 최적의 값을 찾을 수 있다.
ex.
f(x, y) = y - x - 2 * x^2 - 2 * x * y - y^2
x = -2 to 2, y = 1 to 3
single maximum 1.5 -> x = -1, y = 1.5
x = xl + (xu - xl) / r = -2 + 4r
y = yl + (yu - yl) / r = 1 + 2r

▶Univariate and Pattern Search
univariate search 방법은 근사치를 개선하기 위해 한 번에 하나의 변수를 변경하는 것이다.
단 하나의 변수만 변경되기 때문에, one-dimensional search로 감소한다.
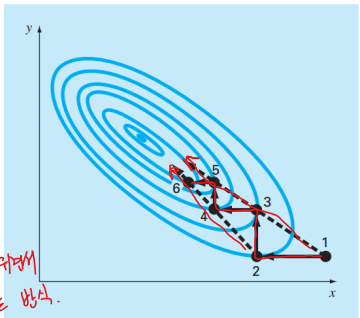
점점 최대치를 향해 나아가고 있지만, 최대치를 향해 좁은 능선을 따라 움직일 때 효율성이 떨어진다.
그러나 1-3, 3-5 또는 2-4, 4-6과 같은 점을 연결하는 선은 최댓값의 일반적인 방향을 가리킨다.
능선을 따라 최대 방향으로 직접적으로 향할 수 있다.
pattern directions라고 한다.

formal algorithm은 최적의 값을 효율적으로 찾기 위해 패턴 방향을 이용할 수 있다.
이 알고리즘들 중 가장 잘 알려진 것은 Powell's method이다.
1차원 검색을 통해 얻은 1과 2로 형성된 선이 최대 방향으로 향한다. (위 그림)
그러한 선들은 conjugate direction이라고 불린다.
▶Powell's method
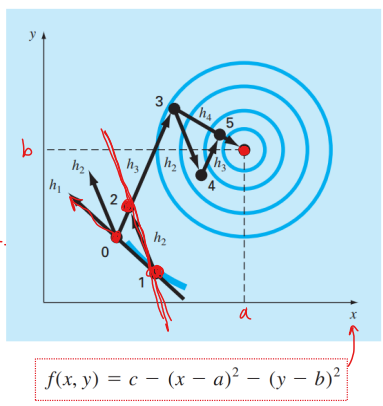
algorithm summary
1. x0을 시작점으로 두고 방향이 다른 h1, h2 벡터를 잡는다.
2. x0을 시작으로 1D에서 h1방향으로 최적의 값 x1을 구한다.
3. x1을 시작으로 1D에서 h2방향으로 최적의 값 x2를 구한다.
4. h3는 x0과 x2가 이루는 방향이다.
5. x2를 시작으로 1D에서 h3방향으로 최적의 값 x3를 구한다.
6. x3를 시작으로 1D에서 h2방향으로 최적의 값 x4를 구한다.
7. x4를 시작으로 1D에서 h3방향으로 최적의 값 x5를 구한다.
8. h4는 x3와 x5가 이루는 방향이다.
9. x5를 시작으로 1D에서 h4방향으로 최적의 값이 xopt이다.
Powell's method는 미분 계산 없이 수렴한다.
'컴퓨터공학 > 수치해석' 카테고리의 다른 글
| [수치해석] Ch14. Grandient Methods - Multidimensional (0) | 2022.12.10 |
|---|---|
| [수치해석] Ch13. One-Dimensional Unconstrained Optimization (0) | 2022.12.10 |
| [수치해석] Ch7. Roots of Polynomials (0) | 2022.12.10 |
| [수치해석] Ch6. Open Method (0) | 2022.10.20 |
| [수치해석] Ch5_2. Roots of Equations - False Position Method (0) | 2022.10.20 |