728x90

복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
다항식의 근은 세가지 규칙을 따른다.1. n차 방정식의 경우, n개의 실근과 허근을 가진다.(근들이 반드시 구별되는 것은 아니다.)2. n이 홀수면, 적어도 하나의 실근을 가진다.(complex root(허근)은 +- 한쌍을 가지기 때문에 남는 하나는 실근이 된다.)3. 허근이 존재하면, 한 쌍으로 존재한다.(λ + μi와 λ - μi, i는 root(-1))
▶Synthetic division
연산을 수행하기 위해 여러 컴퓨터 알고리즘(합성 분할 및 기타 방법에 기반)을 사용할 수 있습니다.
n차 다항식을 단항 인자 (x - t)로 나누는 다음과 같은 유사 코드에 의해 하나의 간단한 체계가 제공된다.
# 슈도코드
r = a(n)
a(n) = 0
do for i = n-1, 0, -1
s = a(i)
a(i) = r
r = s + r * t
end do# divide function f(x) = (x-4)(x+6) = x**2 + 2*x - 24
# by the factor x-4
#f(x)를 x-4로 나누기
#x - t로 나누는 것임.
t = 4
a = [-24, 2, 1] # f(x) 각 term들의 계수를 입력
n = 2
r = a[n]
a[n] = 0
for i in range(n-1, -1, -1):
s = a[i]
a[i] = r
r = s + r * t
print(f"s:{s}, a[{i}] : {a[i]}, r : {r}")
print(a,r)
아래 슈도코드의 서브루틴은 n차 다항식 a를 m차 다항식 d로 나누는 일반적인 문제를 다룬다.
결과는 (m - 1)차 다항식을 나머지로 하는 (n - m)차 다항식 q이다.
sub poldiv(a, n, d, m, q, r)
dofor j = 0, n
r(j) = a(j)
q(j) = 0
end do
dofor k = n-m, 0, -1
q(k+1) = r(m+k) / d(m)
dofor j = m+k-1, k, -1
r(j) = r(j) - q(k+1) * b(j-k)
end do
end do
dofor j = m, n
r(j) = 0
end do
n = n - m
dofor i = 0, n
a(i) = q(i+1)
end do
end sub728x90
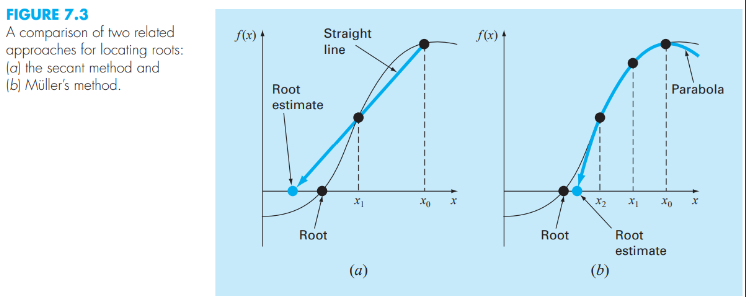
▶Muller's Method
세 점을 통과하는 포물선 계수를 도출하는 방식이다..
그런 다음 이 계수들을 4차 공식으로 대체하여 포물선이 x 절편, 즉 루트 추정치를 얻을 수 있다.
접근법은 포물선 방정식을 편리한 형태(f2(x) = a(x - x2)^2 + b(x - x2) + c)로 작성함으로써 촉진된다.
포물선은 세 점([ x0, f(x0) ], [ x1, f(x1) ], [ x2, f(x2) ])과 교차한다.
a, b, c는 세 점을 각각 대입하여 구할수 있다.
슈도코드
sub muller(xr, h, eps, maxit)
x2 = xr
x1 = xr + h*xr
x0 = xr - h*xr
do
iter = iter + 1
h0 = x1 - x0
h1 = x2 - x1
d0 = (f(x1) - f(x0)) / h0
d1 = (f(x2) - f(x1)) / h1
a = (d1 - d0) / (h1 + h0)
b = a * h1 + d1
c = f(x2)
rad = sqrt(b*b - 4*a*c)
if abs(b+rad) > abs(b-rad) then
den = b + rad
else
den = b - rad
end if
dxr = -2*c / den
xr = x2 + dxr
print iter, xr
if(abs(dxr) < eps*xr or iter >= maxit)
exit
x0 = x1
x1 = x2
x2 = xr
end do
end mullerex.
x0, x1, x2 = 4.5, 5.5, 5
f(x) = x^3 - 13x - 12
roots = -3, -1, 4
import math
# Muller's Method
# f(x) = x**3 - 13*x - 12
# x0 = 4.5, x1 = 5.5, x2 = 5
# roots are -3, -1, 4 -> (x+3)(x+1)(x-4)
def func_f(x):
ff= x**3 - 13*x - 12
return ff
xr = 5
h = 0.1
eps = 0.00000000001
maxit = 100
x2 = xr
x1 = xr + h*xr
x0 = xr - h*xr
print("---------------------------------")
print(f"x0 : {x0}, x1 : {x1}, x2 : {x2}")
print("---------------------------------")
iter = 0
while True :
iter = iter + 1
h0 = x1 - x0
h1 = x2 - x1
d0 = (func_f(x1) - func_f(x0)) / h0
d1 = (func_f(x2) - func_f(x1)) / h1
a =(d1 - d0) / (h1 + h0)
b = a*h1 + d1
c = func_f(x2)
rad = math.sqrt(b*b - 4*a*c)
if abs(b+rad) > abs(b-rad) :
den = b + rad
else :
den = b - rad
dxr = -2*c / den
xr = x2 + dxr
print( f"Iter : {iter}, xr : {xr}, dxr : {dxr}")
if abs(dxr) < eps*xr or iter >= maxit :
break;
x0 = x1
x1 = x2
x2 = xr
print("")
print(f"xr : {xr}")
728x90
'컴퓨터공학 > 수치해석' 카테고리의 다른 글
| [수치해석] Ch14. Directed Methods - Multidimensional (0) | 2022.12.10 |
|---|---|
| [수치해석] Ch13. One-Dimensional Unconstrained Optimization (0) | 2022.12.10 |
| [수치해석] Ch6. Open Method (0) | 2022.10.20 |
| [수치해석] Ch5_2. Roots of Equations - False Position Method (0) | 2022.10.20 |
| [수치해석] Ch5_1. Roots of Equations - Bisection Method (0) | 2022.10.20 |