
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶Contents
- 최단경로
- Bellman-Ford algorithm
- Dijkstra algorithm
- Acyclic Shortest Path
- Seam Carving
▶Shortest Path(Edge-Weighted Digraph)
<입력>
간선에 weight가 있는 directed graph G
<출력 : 출발지 s에서 도착지 t까지 최단경로>
s에서 t까지 연결하는 경로 중 (연결된 간선의 집합) 간선의 weight 합이 최소인 경로
weight 합이 0보다 작은 사이클이 있는 그래프는 최단 경로로 존재하지 않는다.
사이클이 있어도 최단 경로는 존재한다.
weight가 0보다 작은 간선이 있어도 최단 경로는 존재한다.
하지만, 간선의 weight를 모두 더한 총합이 음수인 사이클이 있으면 최단경로는 존재할 수 없다.
그 지역만 뺑뺑 돌 수도 있기 때문이다.


source-sink와 all pairs는 single source를 이용해 풀 수 있다.
single sink는 single source의 역 그래프를 이용하면 풀 수 있다.
single source 문제의 해는 어떤 자료 구조에 저장하나?
<방법 1> 각 목적지마다 최단 경로 저장(거쳐가는 정점 or 간선의 리스트 형태로)


<방법 2> SPT(Shortest Path Tree) 형태로 저장한다.
why? single source 문제의 해는 하나의 트리로 표현되기 때문이다.

정점 s~t까지 최단경로의 일부 역시 최단경로이다.
s~t과정에 k를 거친다면, s~k 역시 k까지의 최단경로이다.
<자료구조>
edgeTo[] : s~v 최단 경로에 사용된 마지막 간선
distTo[] : s~v 최단 경로의 길이

def pathTo(self, v):
path = []
e = self.edgeTo[v]
while e != None:
path.append(e)
e = self.edgeTo[e.v]
path.reverse()
return pathedgeTo[]와 distTo[] 만들어 가는 방법
1. 초기화
모든 정점에 대해 edgeTo[] = None
출발지 s의 distTo[s] = 0 / 그 외의 distTo[t] = ∞
2. 탐색
기존에 알던 s-t경로보다 더 짧은 경로를 발견하면 edgeTo[t], distTo[t] 업데이트
distTo[t] : 현재까지 발견한 t까지 최단거리
edgeTo[t] : 현재까지 발견한 t까지 최단 경로에서 마지막 간선
3. 완료
모든 가능한 경로 탐색이 끝났다면
distTo[t] : t까지 최단거리
edgeTo[t] : t까지 최단 경로에서 마지막 간선
t까지 경로 탐색: s부터 t까지 처음부터 경로 구성하는 대신
기존에 알고 있던 경로 s~v에 간선 e=v→t 더해 새 경로 P=s~t 구성
기존에 알고 있던 경로 P’:s~t 보다 P가 더 짧다면 P’를 P로 대체
relax(e)
기존에 알던 s-v 경로에 간선 e=v-t 더했을 때 t까지 더 짧은 경로가 나온다면,
이 경로를 edgeTo[t], distTo[t]에 저장한다.
def relax(self, e):
if self.distTo[e.t] > self.distTo[e.v] + e.weight:
self.distTo[e.t] = self.distTo[e.v] + e.weight
self.edgeTo[e.t] = ee=v->t relax 할 때, v까지 경로를 아직 모른다면 (dist[t]=∞)
지금까지 발견된 t까지 경로보다 짧아질 수 없어 edgeTo[], distTo[] 변화가 없다.
relax(x->v)에 의해 v까지 경로가 더 짧은 경로로 변경되었다면
v에서 나가는 각 간선 e=v->w를 다시 relax 해서 w까지의 경로도 수정해야 한다.
v까지의 최단 경로 계산 후에 v에서 나가는 각 간선 e=v->w를 relax 한다면
e를 단 한 번만 relax 하면 되어 효율적으로 될 것이다.
<정리>
1. 최단 경로는 트리 형태로 저장한다.
2. SPT를 얻기 위해 적절한 순서로 간선 relax 하는 일을 반복한다.
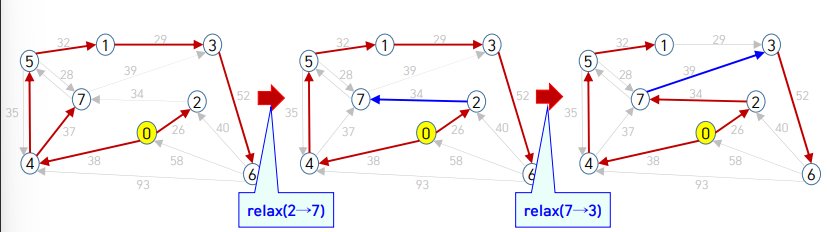
relax(v) : 정점 v에서 outgoing 하는 모든 간선 e=v->w를 relax 한다.
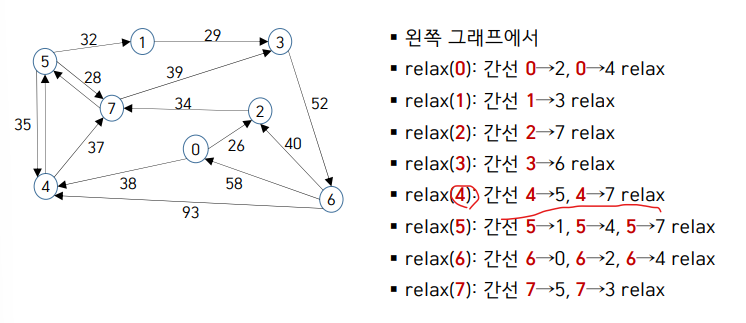
▶Bellman-Ford 알고리즘
초기화
(모든 정점에 대해) edgeTo[] = None
(출발지 s) distTo[s]=0, (그 외) distTo[t]=∞
다음을 V-1회 반복한다. (V: 정점 개수)
모든 정점 relax (=모든 간선 relax)
# g: EdgeWeightedDigraph 객체
for _ in range(g.V)-1:
for v in range(g.V):
for e in g.adj[v]: relax(e)최대 ~V*E 시간을 소요한다.
다익스트라 : 비중 >=0 경우
Acycle : 사이클이 없는 경우
벨만 포드 : 모든 경우 다 가능
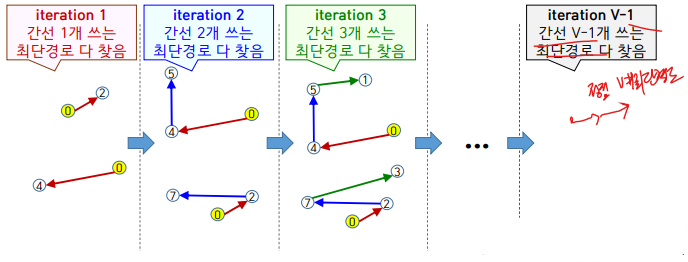
10장 27~30 페이지 이해 안 된다. 다시 보기.
▶Dijkstra 알고리즘
v까지의 최단 경로 계산 끝난 후에 v에서 나가는 각 간선 e=v->w를 relax 한다면
e를 단 한 번만 relax 하면 되어 효율적이게 된다.
초기화
(모든 정점에 대해) edgeTo[] = None, (출발지 s) distTo[s]=0, (그 외) distTo[t]=∞
출발지 s에서 먼저 도달할 수 있는 정점 순으로 선정한다.
선정한 정점 v를 SPT에 포함한다.
v로부터 outgoing 하는 각 간선 e=v→t에 대해 t가 아직 SPT에 포함되지 않았다면 e를 relax
relax 한 relax 한 간선은 더는 relax하지 않는다.
따라서 bellman-ford보다 효율적이다.
class DijkstraSP(SP): # Inherit SP class
def __init__(self, g, s):
super().__init__(g, s) # run the constructor of the parent class
self.pq = IndexMinPQ(g.V)
self.pq.insert(s, 0)
while not self.pq.isEmpty():
# select vertices in order of distance from s
dist, v = self.pq.delMin()
for e in self.g.adj[v]:
self.relax(e)
def relax(self, e):
if self.distTo[e.w] > self.distTo[e.v] + e.weight:
self.distTo[e.w] = self.distTo[e.v] + e.weight
self.edgeTo[e.w] = e
if self.pq.contains(e.w): self.pq.decreaseKey(e.w, self.distTo[e.w])
else: self.pq.insert(e.w, self.distTo[e.w])
Dijstra 알고리즘은 minpq 성능에 의존한다
| Operation | 1회 비용 | 필요한 횟수 |
| PQ, insert | logV | V |
| PQ, deleteMin | logV | V |
| PQ, decreaseKey | logV | E |
~ElogV
| Bellman-Ford | Dijkstra | |
| 방법 | E개 간선 모두를 relax 하는 것 정점 수 V-1회 반복 |
출발지 s에서 가까운 정점 v 순으로 v의 모든 간선 relax |
| 시간복잡도 | ~E*V | ~ElogV |
| 간선에 negative weight 허용? | (한번 거친 곳도 다시 relax 하므로) 음수 weight인 간선 있어도 동작 |
(한번 지나간 곳은 다시 보지 않으므로) 간선 weight>= 0인 경우만 최단 경로 찾음 음수 weight 있따면 iteration 지날 때마다 더 먼 경로 발견한다는 가정 어긋남 |
| Cycle 허용? | yes. cycle있는 directed graph에서도 최단경로 찾음 |
yes. cycle있는 directed graph에서도 최단 경로 찾음 |
▶Acyclic Shortest Path
사이클이 존재하지 않는다면 벨만 포드나 다익스트라보다 더 간단하게 찾을 수 있다.
Topological order
v->w 경로가 있다면 v 후에 w가 오도록 하는 순서
Topological order 순으로 정점 나열하는 것을 topological sort라고 한다.
초기화
(모든 정점에 대해) edgeTo[] = None, (출발지 s) distTo[s]=0, (그 외) distTo[t]=∞
Topological order 순으로 정점 v 선정한다.
v로부터 outgoing 하는 모든 간선 e=v→t
class AcyclicSP(SP):
def __init__(self, g, s):
super().__init__(g, s) # run the constructor of the parent class
tpOrder = topologicalSort(g)
for v in tpOrder:
for e in self.g.adj[v]:
self.relax(e)DFS 하는 ~V+E만큼 시간을 소모한다.
그렇기에 사이클이 없다면 다른 알고리즘보다 효율적이다.
| Bellman-Ford | Dijkstra | Acyclic SP | |
| 방법 | E개 간선 모두를 relax 하는 것 정점 수 V-1회 반복 |
출발지 s에서 가까운 정점 v 순으로 v의 모든 간선 relax |
Topological order 순으로 정점 v를 선택해 v의 모든 간선 relax |
| 시간복잡도 | ~E*V | ~ElogV | ~E+V |
| 간선에 negative weight 허용? | (한번 거친 곳도 다시 relax 하므로) 음수 weight인 간선 있어도 동작 |
(한번 지나간 곳은 다시 보지 않으므로) 간선 weight>= 0인 경우만 최단 경로 찾음 음수 weight 있따면 iteration 지날 때마다 더 먼 경로 발견한다는 가정 어긋남 |
(한번 지나간 곳은 다시 돌아오는 길이 없어서) 음수 weight인 간선 있어도 동작한다. |
| Cycle 허용? | yes. cycle있는 directed graph에서도 최단경로 찾음 |
yes. cycle있는 directed graph에서도 최단 경로 찾음 |
no. cycle있으면 topological order이 존재하지 않는다. |
'컴퓨터공학 > 알고리즘2' 카테고리의 다른 글
| [알고리즘2] Max Flow and Min Cut (0) | 2022.12.10 |
|---|---|
| [알고리즘2] Seam Carving 구현 - 실습 (1) | 2022.12.09 |
| [알고리즘2] Prim's Algorithm의 Eager Version 구현 - 실습 (1) | 2022.12.08 |
| [알고리즘2] Minimum Spanning Tree(MST) (0) | 2022.12.08 |
| [알고리즘2] Cycle Detection and WordNet (0) | 2022.11.26 |