
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶Contents
- WordNet
- Outcase
- SCA & SAP
- WordNet과 outcaset 탐지 구현
▶WordNet
정점(synset) : 유사어(synonym)의 집합(set)
v -> w 간선 : v is a w 관계 (hyponym -> hypernym)
- 'apple' is an edible fruit
- 'banana' is an edible fruit

WordNet의 특성
Cycle이 없다. (DAG, Directed Acyclic Graph)
Root는 하나이다. (entity)
부모가 둘 이상인 경우도 있고, 자식이 둘 이상인 경우도 있다.
같은 단어가 여러 다른 정점에 나타나기도 한다.
-> 다른 의미를 나타낼 수도 있기 때문이다. (집고양이, 빅켓(고양잇과 동물))
▶Outcast
단어 집합에서 다른 언어와 가장 의미가 다른 단어
ex. horse, zebra, cat, bear, table 중 가장 관련이 적은 단어는 table이다. table이 outcast

Outcast 탐지 방법
distance(wa, wb) 계산 방법
같은 정점에서 만날 때까지 wa, wb 각각에서 간선 따라 올라간 후, 거쳐온 간선 수 더한다.
common ancestor(공통 조상) : 두 탐색이 만난 정점
ancestral path(공통 조상까지 경로) : wa, wb에서 공통 조상까지 거쳐온 경로

distance(wa, wb) : shortest common ancestor까지 거리
같은 단어 wb, wb에 대해 공통 조상과, 조상까지 경로는 둘 이상일 수 있다.
1) 부모 둘 이상일 수도 있고
2) 같은 단어가 여러 정점에 있을 수도 있으므로
이중 가장 가까운 조상까지 거리를 distance로 사용한다.
SCA (Shortest Common Ancestor, 가장 가까운 공통 조상) : 두 탐색이 만나는 가장 가까운 정점
SAP (Shortest Ancestral Path, SCA까지 경로) : wa, wb에서 SCA까지 거쳐온 경로
# 구현해야 하는 기능
def sap(g, aList, bList):
# g: Digraph 객체, aList: 정점 번호 목록, bList: 정점 번호 목록
# Digraph g 탐색해 aList 속한 정점과 bList 속한 정점 간
# SCA(가장 가까운 조상) 하나와 SCA까지 거리 반환sapLength = math.inf # 지금까지 찾은 SAP의 최소 길이
# 무한대로(∞) 초기화
aList, bList 원소 모두 Q에 추가
while Q is not empty:
v = Q.get()
v까지 거쳐온 거리 >= sapLength: break # 탐색 중단
for w in g.adj[v]: # v→w 간선 있는 각 정점 w에 대해
if v에 aList로부터 왔다면:
w에 aList로부터 도달한 적 없다면
w를 aList로부터 방문한 것으로 표기하고 Q.put(w)
w에 bList로부터 방문했었다면 SAP 길이 구해서
sapLength보다 더 작다면 update
elif v에 bList로부터 왔다면:
w에 bList로부터 도달한 적 없다면
w를 bList로부터 방문한 것으로 표기하고 Q.put(w)
w에 aList로부터 방문했었다면 SAP 길이 구해서
sapLength보다 더 작다면 update2개 이상의 노드로부터 탐색을 해야 하기 때문에 multi-source BFS를 수행한다.
따라서 시간은 ~(V + E)에 비례한다.
▶WordNet 그래프 구현
synsets.txt : WordNet의 정점에 대한 정보
한 라인에 정점 하나의 정보를 포함한다.
라인 형식 : [정점 번호], [정점에 포함되는 유사어 집합(공백으로 구분)], [의미]
[정점 번호] : 0 ~ 82191
[정점에 포함되는 유사어 집합] : 1 ~ 28개
hypernyms.txt : WordNet의 간선 정보. hyponym(부분 집합) -> hypernym(더 큰 집합) 관계
한 라인에 정점 하나에서 나가는 모든 간선 (outgoing edges) 정보 포함
라인 형식 : [정점 v 번호], [정점 w1 번호], [정점 w2 번호], [정점 w3 번호], …
다음과 같은 간선 있음 의미 : v -> w1, v -> w2, v -> w3, …
outdegree(v) : 0~6
1) Digraph self.g
기존 Digraph 클래스로 숫자 정점 가진 그래프 표현
기존에 Digraph에 대해 작성 한 기능 재활용 가능하므로 작 성할 코드 줄어들고,
숫자 그 래프에 대한 SCA&SAP 탐색도 가능하다.
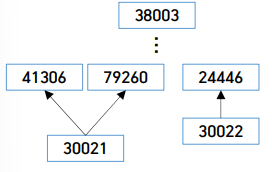
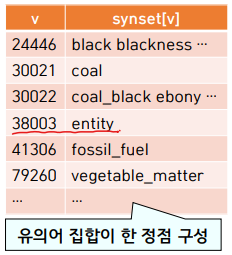
2) 리스트 self.synsets
synset[v] : 정점번호 v 의미하는 유사어 집합(synset) 저장
정점 번호 주어졌을 때 대응되는 단어 찾기 위해서
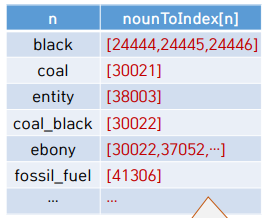
3) 심볼테이블 self.nounToIndex
nounToIndex[n] : 단어 n에 대응되는 정점번호 목록
단어 주어졌을 때 대응되는 정점 찾기 위해서
'컴퓨터공학 > 알고리즘2' 카테고리의 다른 글
| [알고리즘2] Prim's Algorithm의 Eager Version 구현 - 실습 (1) | 2022.12.08 |
|---|---|
| [알고리즘2] Minimum Spanning Tree(MST) (0) | 2022.12.08 |
| [알고리즘2] DirectedGraph에 SCC 구현 - 실습 (1) | 2022.11.22 |
| [알고리즘2] Undirected and Directed Graphs (1) | 2022.11.22 |
| [알고리즘2] Slider Puzzle 구현 with PQ - 실습 (0) | 2022.10.21 |