728x90

복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶관계형 대수 (Relational Algebra)
- 릴레이션을 처리하기 위한 연산자들의 집합
- 연산의 피연산자가 모두 릴레이션이고 연산 결과 또한 릴레이션이다.
- 집합 연산자
- 합집합 (Union ∪)
- 교집합 (Intersect ∩)
- 차집합 (Difference -)
- 곱집합 (Cartesian Product X)
- 순수 관계형 연산자
- 실렉트 (Select)
- 프로젝트 (Project)
- 조인 (Join)
- 디비전 (Division ÷)
▶집합 연산자
- 곱집합(카티션 프로덕트)을 제외하고는 피연산자인 두 릴레이션은 서로 합병 가능해야 한다.
- 합병가능(Union-Compatible)
- 두 릴레이션 R과 S가 있을 때 차수가 같고(애트리뷰트의 개수),
- 대응되는 애트리뷰트의 도메인이 같아야 한다.
- 합집합, 교집합, 곱집합 연산은 결합적이다.
- 합집합, 교집합, 곱집합 연산은 교환적이다.
- 합병가능(Union-Compatible)
- 곱집합(Cartesian product)
- R에 속한 각 튜플 r과 S에 속한 각 튜플 s에 대해 모든 가능한 조합으로 접속시킨 r·s로 구성된 릴레이션이다.
- 결과 릴레이션 : R차수와 S차수의 합과 같다.
- 카디널리티는 |R x S| = |R| x |S|가 된다.

▶순수 관계형 연산자
- 관계형 데이터베이스에 적용할 수 있도록 특별히 고안한 연산자들이다.
- 실렉트, 프로젝트, 조인, 디비전이 있다.
728x90
▶실렉트 (Select)
- 주어진 선택 조건을 만족하는 튜플들을 선택하는 연산자이다.
- 수평적 부분집합을 찾는다고 볼 수 있다.
- 시그마 기호를 입력할 수 없어서 @로 대체해서 쓰겠다.
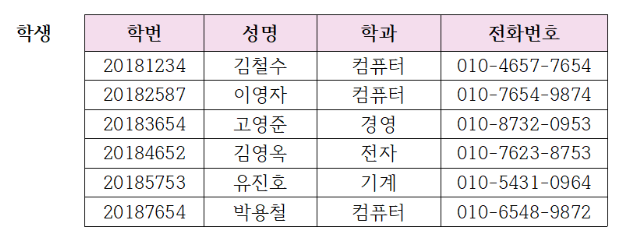
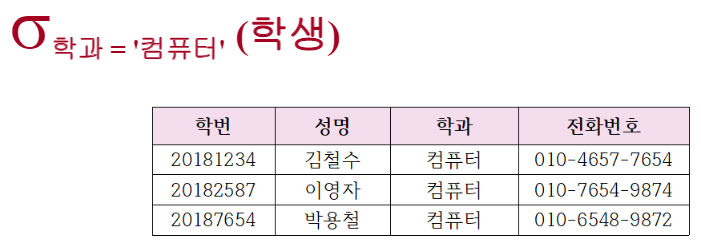
- A와 B를 릴레이션 R의 애트리뷰트라 할 때,
- @Aθc(R)={ r | r ∈ R ∧ r[A] θ c }
- @AθB(R)={ r | r ∈ R ∧ r[A] θ r[B] }
- θ(theta) : 비교 연산자(<, >, ≤, ≥,=, ≠)
- c : 상수
- r : 릴레이션 R의 튜플
- Aθc, AθB : 비교식, 조건식, 또는 프레디킷(predicate)
- 실렉트(@)는 프레디킷을 만족하는 튜플을 선택하는 것
- 데이터 언어 형식으로 표현하면 → R where 조건식
- select * from student where 학과="컴퓨터"
▶프로젝트 (Project : pi)
- 기호를 입력할 수 없어서 PI로 대체해서 쓰겠다.
- 주어진 선택 조건을 만족하는 애트리뷰트들을 선택하는 데 사용하는 연산자
- 수직적 부분집합을 찾는다고 볼 수 있다.
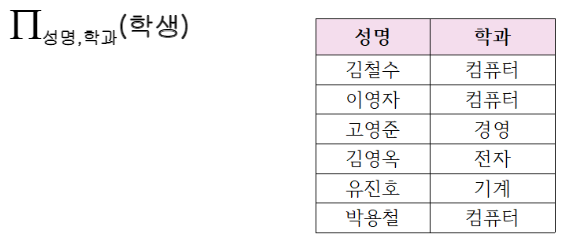
- 전체 애트리뷰트 A의 부분집합 X가 {B1, B2,..., Bm}일 경우, 즉 X = {B1, B2,..., Bm}이고 X ⊆ {A1, A2,..., An}이면,
- PIx(R)={ (r[B1],..., r[Bm] | r ∈ R}]
- 결론적으로, PI성명, 학과(학생)는 학생(학번, 성명, 학과, 전화번호) 릴레이션에서 성명과 학과 애트리뷰트만 추출해내기 때문에 릴레이션에 대한 수직적 연산으로 볼 수 있다.
▶조인 (Join)
- 기호를 입력할 수 없어서 |><|로 대체해서 쓰겠다.
- 학생과 수강 릴레이션에서 학번이 같은 튜플들을 검색해보자.
- 학생 |><|학번=학번 수강
- 학생. 학번과 수강. 학번은 같은 정보인데 중복해서 나오게 된다.

- 두 릴레이션 R과 S가 있다고 하자.
- R |><|AθB S = { r · s | r∈R ∧ s∈S ∧ ( r[A] θ s[B]) }
- 조인 결과
- 릴레이션 R의 튜플 r과 릴레이션 S의 튜플 s에 대해 조인 조건 r[A] θ s[B]를 만족하는 모든 r과 s를 접합해서 만들어지는 튜플로 된 릴레이션
- 동일 조인(equijoin)
- θ가 "="인 조인을 말한다.
- ex. 학생 |><|학번=학번 수강
- 위 ex의 문제점
- 같은 애트리뷰트(즉, 학번)가 결과 릴레이션에 중복되게 나타난다.
▶자연 조인 (natural join)
- 기호를 입력할 수 없어서 |><|N로 대체해서 쓰겠다.
- 동일 조인의 결과에서 중복되는 애트리뷰트를 제거한 조인이다.
- 연산 기호로 |><|N를 사용한다.

▶디비전 (Division : ÷)
- R의 차수가 (m+n)이고 S의 차수가 n이면 R÷S = (m+n) ÷ n = m의 차수가 된다.
- 즉, 두 릴레이션의 공통 도메인 속성의 값이 서로 같은 m의 속성 값을 구하는 것이다.

- 수강(EN) 릴레이션을 코드1(C1)으로 디비전 하라.
- EN ÷ C1
- 코드1에 속해 있는 'CO123'을 수강하고 있는 학생의 학번을 구하는 것이다.
- S100, S300, S400이 검색된다.
- EN ÷ C1
- 수강(EN) 릴레이션을 코드3(C3)으로 디비전 하라.
- EN ÷ C3
- 코드3에 속해 있는 'CO234', 'CO423', 'EE123'을 모두 수강하고 있는 학생의 학번을 구하는 것이다.
- 학번 S400만 검색된다.
- EN ÷ C3
728x90
'컴퓨터공학 > 데이터베이스' 카테고리의 다른 글
| [데이터베이스] 관계형 해석 (0) | 2022.10.18 |
|---|---|
| [데이터베이스] 추가된 관계형 대수 (2) | 2022.10.15 |
| [데이터베이스] 관계형 데이터베이스 (0) | 2022.10.14 |
| [데이터베이스] B 트리 & B+ 트리 (0) | 2022.10.14 |
| [데이터베이스] 물리적 데이터 (0) | 2022.10.13 |