▶배달 - Summer/Winter coding(~2018) (level 2)

▶문제
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
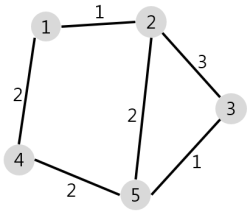
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
▶제한사항
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는 데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
- K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을 간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
▶출력

입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.
▶풀이
다익스트라를 알면 간단하게 풀 수 있는 문제이다.
이전에 백준에서도 다익스트라를 몇 문제 풀었고, 블로그에 쓴 글도 있다.
2022.06.15 - [BOJ Code/Platinum] - [백준/BOJ] platinum4 - 1854번 K번째 최단경로 찾기 (Python)
[백준/BOJ] platinum4 - 1854번 K번째 최단경로 찾기 (Python)
▶1854 - K번째 최단경로 찾기 ▶문제 봄 캠프를 마친 김진영 조교는 여러 도시를 돌며 여행을 다닐 계획이다. 그런데 김 조교는, '느림의 미학'을 중요시하는 사람이라 항상 최단경로로만 이동하
dhalsdl12.tistory.com
이 외에도 두 문제 정도 더 있는데, 이게 내가 쓴 블로그 글 중에서 가장 난이도 있는 다익스트라 문제였다.
아마 이것을 풀 수 있다면 이번 문제도 쉽게 풀 수 있을 것이다.
import sys
import heapq
def dijkstra(dp, graph):
queue = []
heapq.heappush(queue, [0, 1])
while queue:
cur_dist, node = heapq.heappop(queue)
for c, n in graph[node]:
w_dist = cur_dist + c
if w_dist < dp[n]:
dp[n] = w_dist
heapq.heappush(queue, [w_dist, n])
def solution(n, road, K):
answer = 0
graph = [[] for _ in range(n + 1)]
dp = [sys.maxsize for _ in range(n + 1)]
dp[1] = 0
for r in road:
graph[r[0]].append([r[2], r[1]])
graph[r[1]].append([r[2], r[0]])
dijkstra(dp, graph)
for d in dp:
if d <= K:
answer += 1
return answer이번 문제 역시 따로 효율성 테스트는 없는 문제였다.
어떤 기준으로 효율성 테스트가 있는지 없는지는 아직 모르겠지만,
주어지는 숫자가 어느 정도의 기준을 넘어선다면, 효율성 테스트가 존재하는 것 같다.
'Programmers Code > Level 2' 카테고리의 다른 글
| [Programmers] level2 - 두 큐 합 같게 만들기 (Python) : 2022 카카오 테크 인턴십 (0) | 2022.08.23 |
|---|---|
| [Programmers] level2 - 올바른 괄호 (Python) : 스택/큐 (0) | 2022.08.19 |
| [Programmers] level2 - 행렬의 곱셈 (Python) : 연습문제 (0) | 2022.07.25 |
| [Programmers] level2 - 게임 맵 최단거리 (Python) : 깊이/너비 우선 탐색(DFS/BFS) (0) | 2022.07.19 |
| [Programmers] level2 - 영어 끝말잇기 (Python) : Summer/Winter coding(~2018) (0) | 2022.07.18 |