▶1915 - 가장 큰 정사각형

▶문제
n×m의 0, 1로 된 배열이 있다. 이 배열에서 1로 된 가장 큰 정사각형의 크기를 구하는 프로그램을 작성하시오.
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
위와 같은 예제에서는 가운데의 2×2 배열이 가장 큰 정사각형이다.
▶입력
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
▶출력
첫째 줄에 가장 큰 정사각형의 넓이를 출력한다.
▶예제
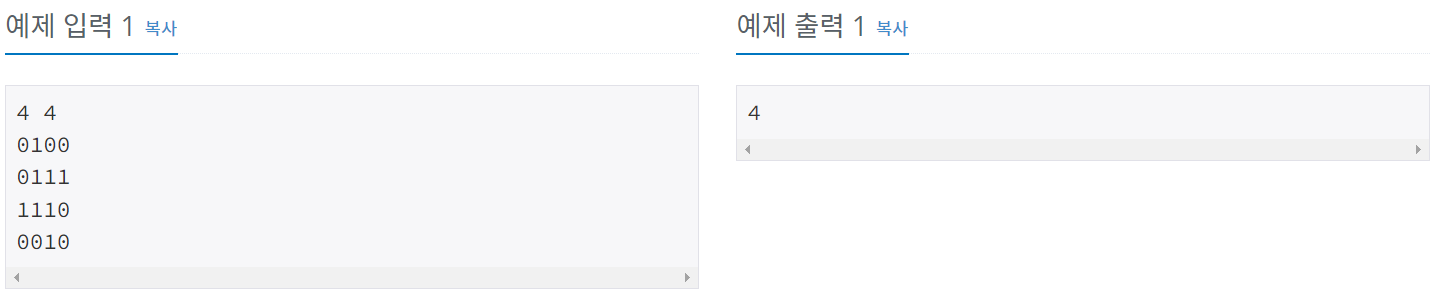
▶풀이
가로세로 길이가 1인 부분은
| 1 |
이렇게 될 것이고,
가로세로 길이가 2인 부분은
| 1 | 1 |
| 1 | 1 |
이 형식이 된다.
그럼 이것을 dp로 바꾸면 되는데, (0,0)에서 (n-1, m-1)까지 비교해준다.
이때 i, j 중 하나가 0이면 그냥 arr 값을 dp에 넣어주고, 그리고 arr가 0일 땐 그냥 0을 넣어준다.
혹은 주변의 값에 따라서 dp값을 넣어주면 된다.
2일 땐
| 1 | 1 |
| 1 | 2 |
3일 땐
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 1 | 2 | 3 |
그 칸 주변 칸의 값들 중 min값에 1을 더한 값을 넣어주면 될 것이다.
그 칸이 1인데 주변이 채워지지 않는다면 그 칸의 dp는 0 + 1이 된다.
이렇게만 해주면 정답이 나온다.
n, m = map(int, input().split())
arr = []
for i in range(n):
a = []
b = int(input())
for j in range(m):
a.append(b // (10 ** (m - j - 1)))
b %= (10 ** (m - j - 1))
arr.append(a)
dp = [[0 for _ in range(m)] for _ in range(n)]
Max = 0
for i in range(n):
for j in range(m):
if i == 0 or j == 0:
dp[i][j] = arr[i][j]
elif arr[i][j] == 0:
dp[i][j] = 0
else:
dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1
if Max < dp[i][j]:
Max = dp[i][j]
print(Max ** 2)
dp를 이용해서 풀었는데, 처음에 세 번이나 틀렸다.
분명히 dp 관계식은 잘 계산해서 넣었는데 자꾸만 틀리게 나왔다.
혹시나 0100을 4개짜리로 나누는 과정에서 문제가 있는가 싶어서 찾아보았는데
for _ in range(n):
arr.append(list(map(int, list(input().rstrip()))))이렇게 하는 방법도 있었다.
나는 그냥 % 해서 하나씩 값을 구해서 넣는 방식을 썼는데, 저 방식을 쓰면 더 나은 거 같았다.
아무튼 그 문제는 아니었고,
if Max < dp[i][j]:
Max = dp[i][j]Max값을 변경해주는 부분에서 처음에 else: 안에 저 코드를 넣었다.
그렇게 하니까 Max값이 변경이 안 되는 부분이 있어서 자꾸 틀렸던 것 같다.
그 부분을 else: 밖으로 빼니까 정답이 나왔다.

이제 85점 남았다. 조금만 더 하면 될 거 같다.
'BOJ Code > Gold' 카테고리의 다른 글
| [백준/BOJ] gold2 - 1398번 동전 문제 (Python) (0) | 2022.07.01 |
|---|---|
| [백준/BOJ] gold4 - 1563번 개근상 (Python) (0) | 2022.06.29 |
| [백준/BOJ] gold4 - 2133번 타일 채우기 (Python) (0) | 2022.06.27 |
| [백준/BOJ] gold4 - 1520번 내리막 길 (Python) (0) | 2022.06.24 |
| [백준/BOJ] gold3 - 2655번 가장높은탑쌓기 (Python) (0) | 2022.06.24 |