
복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.
▶Contents
- Bottom-up Merge Sort
- Sorting Complexity
- Stability of Sorting
- Quick Select
- Duplicate Keys and 3-way Partitioning
▶Merge Sort
인접한 두 조각끼리 Merge(정렬된 순서로 병합)을 반복한다.
총 N개 원소를 병합한다면, 이들을 순서에 맞게 차례로 결과 배열에 옮겨 담으므로 ~N회 작업이 필요하다.
이러한 작업을 ~log(N)회 반복해야 한다.
입력 데이터 크기가 N이라면 결과를 옮겨 담을 ~N의 추가 공간도 필요하다.
# Halve a[lo ~ hi], sort each half and merge,
# using the extra space aux[]
def divideNMerge(a, aux, lo, hi):
if (hi <= lo):
return a
mid = (lo + hi) // 2
divideNMerge(a, aux, lo, mid)
divideNMerge(a, aux, mid+1, hi)
merge(a, aux, lo, mid, hi)
def mergeSort(a):
# Create the auxiliary array once and
# re-use for all subsequent merges
aux = [None] * len(a)
divideNMerge(a, aux, 0, len(a)-1)배열을 나누어가는 과정에서 재귀를 계속해서 호출한다.
-> 시간/공간 overhead가 크다.
이를 해결한 방법이 Bottom-up Merge Sort이다.
Divide 하기 위해 재귀 호출하는 과정을 생략했다. 아래 표와 같이 merge만 수행한다.
sz = 1에서 시작하고, 크기 sz인 인접한 부분끼리만 병합한다.
다음 sz를 2배 해주고 sz >= N 될 때까지 반복한다.
(auz는 ~N 크기의 추가 공간이다.)


<merge 코드 - Bottom-up version에서도 그대로 사용>
# Merge a[lo ~ mid] with a[mid+1 ~ hi],
# using the extra space aux[]
def merge(a, aux, lo, mid, hi):
# Copy elements in a[] to aux[]
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i>mid: a[k], j = aux[j], j+1
elif j>hi: a[k], i = aux[i], i+1
elif aux[i] <= aux[j]: a[k], i = aux[i], i+1
else: a[k], j = aux[j], j+1정렬된 조각 1(a[lo] ~ a[mid])과 정렬된 조각 2(a[mid + 1] ~ a[hi])를 병합한다.
aus는 ~N 크기의 추가 공간이다.
<재귀 호출하는 Top-down version>
# Halve a[lo ~ hi],
# sort each of the halves,
# and merge them,
# using the extra space aux[]
def divideNMerge(a, aux, lo, hi):
if (hi <= lo):
return a
mid = (lo + hi) // 2
divideNMerge(a, aux, lo, mid)
divideNMerge(a, aux, mid+1, hi)
merge(a, aux, lo, mid, hi)
def mergeSort(a):
# Create the auxiliary array once
# re-use for all subsequent merges
aux = [None] * len(a)
divideNMerge(a, aux, 0, len(a)-1)
<Bottom-up version merge sort>
def mergeSort(a): 11
# Create the auxiliary array
aux = [None] * len(a)
sz = 1
while(sz<len(a)):
for lo in range(0, len(a)-sz, sz*2):
merge(a, aux, lo, lo+sz-1, min(lo+sz+sz-1, len(a)-1))
sz += sz # Multiply by 2Q. merge함수 마지막 인자에 min() 함수를 사용한 이유는?
A. 1, 2, 4, 8...로 진행하는데, 배수로 떨어지지 않을 수도 있기 때문이다.
Q. for(lo = 0; lo < len(a) - sz; lo += sz * 2)에서 lo < len(a) - sz를 한 이유는?
A. 잘 모르겠다.
▶Sorting Complexity
Q. 과연 정렬 알고리즘은 얼마나 빨라질 수 있을까?
A. 최적의 알고리즘을 찾기 위해, 혹은 더 개선할 여지를 발견하기 위해서 노력 중이다.
Q. Merge Sort, Quick Sort는 최적의 속도에 다다랐는가?
A. NlogN까지는 가능하다.
임의의 N개를 대소 비교해 나온 모든 경우의 수에 대해서 일반화해보자.
Q. 깊이가 h인 이진 트리에는 (한번 분기했을 때 깊이가 1이 된다고 가정) 잎이 최대 몇 개인가?
A. 한번 하면 잎의 개수가 2개
2번 하면 (깊이는 2) 2^2 = 4개
...
h번하면 (깊이는 h) 잎의 개수 <= 2^h
=이 아닌 <=인 이유는 빠르게 결괏값이 나오면 더 이상 구분을 안 하기 때문이다.
Q. N개 원소에 대한 모든 가능한 정렬이 잎에 한 번은 나오려면, 잎이 최소 몇 개 있어야 하나?
A. N개의 원소이면 N! 가지가 나오기 때문에 잎의 개수는 N! 보다 크다.
위의 문제와 비교 합치면 N! <= 잎의 개수 <= 2^h이다.
따라서 N! <= 2^h가 된다.
Q. 앞 두 문제의 답으로부터 N(정렬할 원소 개수)과 h(worst-case 비교 횟수) 간 관계를 구해보자.
A. N! <= 2^h
log2 N! <= h = 비교 횟수
log2 N! = log2 (N * (N-1) *... * 1)
= log2 N +... + log2 1
<= log2 N +... + log2 N
= Nlog2 N
따라서 비교 횟수 h는 NlogN이 된다.
N개의 서로 다른 원소가 있는 경우, 최적의 정렬 방법은 ~NlogN회 대소 비교가 필요하다.
merge sort(worst case), quick sort(average case)는 이러한 최저치에 가깝다.
▶Stability of Sorting : 정렬 시 추가로 만족시켜야 할 성질
key : 여러 값으로 이루어진 원소의 경우 (예 : class 객체) 정렬에 사용하는 값
정렬 전후 key가 같은 원소 간 상대 순서 보존하는 성질

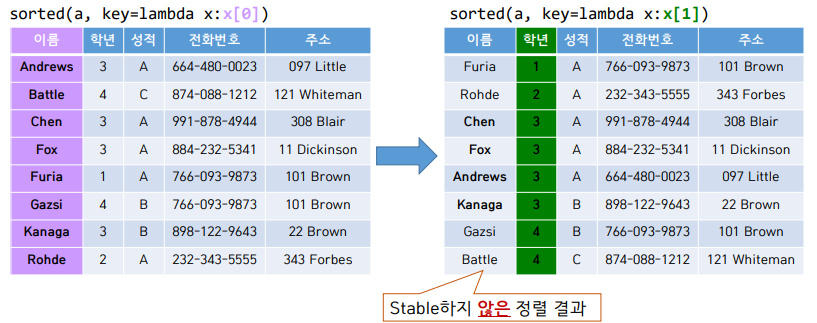
Insertion Sort는 Stable 하다.
iteration i에 이미 정렬된 a[0] ~ a[i-1]에 a[i]를 적절한 위치 (정렬되었을 때의 위치) 찾아서 추가한다.
그 결과 a[0] ~ a[i]까지 정렬된 상태가 된다.

def insertionSort(a):
for i in range(1, len(a)):
key = a[i]
j = i-1
while j>=0 and a[j] > key:
a[j+1] = a[j]
j -= 1
a[j+1] = keyQ. a[j] >= key로 수정해도 stable한가?
A. stable하지 않다.
왜냐하면 같은 E여도 먼저 들어온 E의 위치는 건들면 안 된다.
>=로 하면 E1과 E2는 같기 때문에, 서로 자리가 바뀌게 된다.
그렇기 때문에 stable하지 않게 된다.
Selection Sort는 Stable하지 않다.
iteration i에 a[i] ~ a[N - 1] 중 최솟값을 찾아 a[i]와 swap 해준다.

def selectionSort(a):
for i in range(len(a)-1):
# Find the minimum in a[i]~a[N-1]
min_idx = i
for j in range(i+1, len(a)):
if a[j] < a[min_idx]:
min_idx = j
# Swap the found minimum with a[i]
a[i], a[min_idx] = a[min_idx], a[i]코드의 마지막 부분, 서로 자리를 바꾸는 코드 때문에 stable하지 않게 되는 것이다.
원거리 swap을 하기 때문이다.
가장 작은 값을 앞으로 당겨서 넣는데 그 자리에 B1이 있으면 B1이 뒤로 갈 수 있기 때문이다.
Shell Sort는 Stable하지 않다.
h를 점진적으로 1까지 감소시켜가면서 h-sort를 수행한다.
shell sort는 selection sort의 코드를 가져와 일부 수정해서 만든 것이다.
그렇기에 selection sort처럼 원거리 swap을 하기 때문에 stable하지 않다.
ex. 4-sort : C1 B1 B2 B3 B4 -> B4 B1 B2 B3 C1
ex. 4-sort : B1 B2 B3 B4 A1 -> A1 B2 B3 B4 B1
Merge Sort는 Stable 하다.
크기가 1인 조각에서 시작해 인접한 조각끼리 merge 한다.
# Merge a[lo ~ mid] with a[mid+1 ~ hi],
# using the extra space aux[]
def merge(a, aux, lo, mid, hi):
# Copy elements in a[] to aux[]
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i>mid:
a[k], j = aux[j], j+1
elif j>hi:
a[k], i = aux[i], i+1
elif aux[i] <= aux[j]:
a[k], i = aux[i], i+1
else:
a[k], j = aux[j], j+1코드 13번째 줄에서 <=를 <로 바꾸면 stable 하지 않게 된다.
두 개의 조각을 합쳐야 한다. 왼쪽에 있는 조각이 i를 기준으로, 오른쪽 조각이 인덱스 j부터이다.
만약 i번째와 j번째가 같으면 원래는 i를 집어넣는다.
하지만 <=를 <로 바꾸면 그 코드를 하지 않고 j를 넣는 코드를 하기 때문에, 뒤에 것이 들어가 stable이 깨진다.
Quick Sort는 Stable하지 않다.
# Partition a[lo~hi] using a[lo] as pivot
def partition(a, lo, hi):
i, j = lo+1, hi
while True:
while i<=hi and a[i]<a[lo]:
i = i+1
while j>=lo+1 and a[j]>a[lo]:
j = j-1
if (j <= i):
break # Pointers cross
a[i],a[j] = a[j],a[i] # Swap(a[i],a[j])
i,j = i+1,j-1
a[lo],a[j] = a[j], a[lo] # Swap a[j] with pivot
return j # Return the index of item in place첫 값을 기준으로 작은 값과 큰 값을 구분한다.
그럼 순서에서 첫 값, 작은 값들, 큰 값들이 된다.
다음으로 첫 값을 사이에 넣어서 작은 값, 첫 값, 큰 값들로 구성한다.
처음에 첫 값을 기준으로 구분할 때 원거리 swap을 하게 된다.
뒤에서부터 먼저 나온 작은 값과, 앞에서부터 나온 큰 값이 교환하게 된다.
그럼 작은 값과 같은 값이 중간에 나오게 되면, 순서가 꼬이게 된다.
정렬의 stability는 많은 application에서 중요하다.
merge sort는 효율적일 뿐 아니라 (worst case ~NlogN) stable 해서, 'stability' 요구하는 application에서는 quick sort보다 선호된다.
▶Quick Select
Quick sort
v를 기준 값으로 좌우로 partition후 각 조각을 다시 partition 하는 방식이다.
partition 했을 때 기분 값은 정렬된 위치에 있게 된다.
N=2개의 원소를 partition 하면 정렬이 완료되므로, 좌우 조각을 partition 하다 보면 모든 원소가 정렬된다.
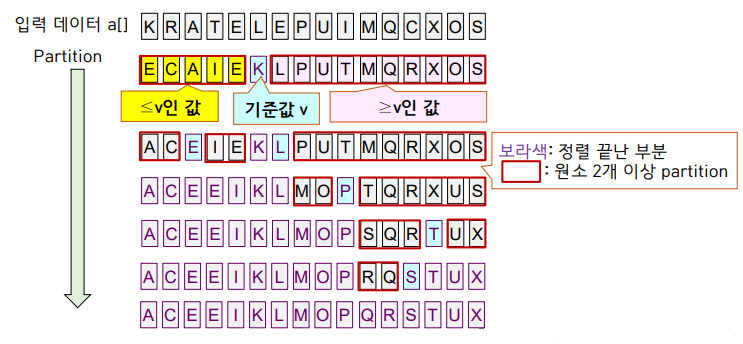
Selection
크기 N의 배열이 주어졌을 때, k번째로 작은 원소 찾기이다. (k는 0부터 시작이다.)
0 <= k <= N-1
k = 0인 경우 : 최솟값(min) 찾기
k = N - 1인 경우 : 최댓값(max) 찾기
k = N / 2인 경우 : 중간값(median) 찾기
quick sort의 방식을 사용하면 된다.
quick sort는 기준 값을 가지고 좌우를 다 partition 하는 방식이라면,
quick select는 원하는 방향만 partition 해주면 된다.
partition 하면 기준 값 a[j]는 정렬된 위치에 있다.
j == k라면 k번째 원소를 찾았기 때문에 a[j]를 반환해준다.
j < k라면 오른쪽 partition만 분할해준다.
j > k라면 왼쪽 partition만 분할해준다.
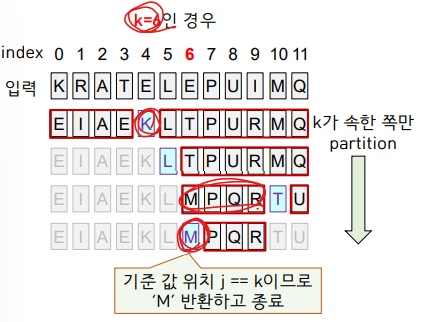
<Quick Sort 코드>
# Partition a[lo~hi] and
# continue to partition each half recursively
def divideNPartition(a, lo, hi):
if (hi <= lo): return
j = partition(a, lo, hi)
divideNPartition(a, lo, j-1)
divideNPartition(a, j+1, hi)
# 양쪽 partition 모두 다시 분할한다.
# 둘 이상 가지로 분기하므로 재귀 호출로 작성하면 편하다.
def quickSort(a):
# Randomly shuffle a,
# so that the partitioning item is chosen randomly
random.shuffle(a)
divideNPartition(a, 0, len(a)-1)
<Quick select 코드>
# Find k-th smallest element,
# where k = 0 ~ len(a)-1
def quickSelect(a, k):
# Randomly shuffle a, so that two
# partitions are equal-sized
random.shuffle(a)
lo, hi = 0, len(a)-1
while (lo < hi):
j = partition(a, lo, hi)
if j<k:
lo = j+1
elif k<j:
hi = j-1
else:
return a[k]
return a[k]배열 a를 shuffle 해야 더 균등하게 분할해서 성능이 좋다.
Quick Select의 성능
N개의 값 partition 위해서 N에 비례한 횟수의 비교/메모리 접근을 수행한다.
N개의 원소를 크기 1이 될 때까지 대략 반으로 나누어간다면,
N + N/2 + N/4 +... + 1 = ~2N에 비례한 횟수의 비교/메모리 접근을 수행한다.
N개의 원소를 partition 해서 크기 N-1인 조각이 계속해서 나오는 경우,
N + N-1 + N-2 +... + 1 = ~n^2 / 2에 비례한 횟수의 비교/메모리 접근을 수행한다.
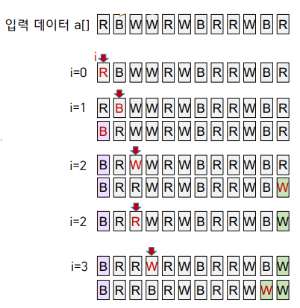
3-Way Partitioning
a[low ~ hi]를 3-way partition 하기 위해 a[low]를 기준 값 v로 정한다.
최종적으로 3개 영역으로 나누고자 한다.
1. 왼쪽→오른쪽 방향으로 한 번에 한 원소 a[i] 검사한다.
2. a[i] < v이면(기준값 보다 작다.) 왼쪽 영역(의 오른쪽 끝 - lt)으로 이동한다.(swap) i++
3. a[i] > v이면(기준값 보다 크다.) 오른쪽 영역(의 왼쪽 끝 - gt)으로 이동한다.(swap)
4. a[i]==v 이면 이동시키지 않는다. i++
5. i가 오른쪽 영역에 들어서면 검사 중단한다.
Q. v보다 작은 값을 왼쪽 영역으로 이동시킬 때는 i++하지만 큰 값을 오른쪽으로 이동시킬 때는 i++하지 않는 이유는?
A. 오른쪽에 있는 값중에서 gt로 지정한 부분을 앞으로 가져오기 때문이다.
그 값은 아직 비교하지 않은 값이기 때문에, 그대로 i값을 가지고 v와 비교해주어도 되기 때문이다.
하지만, v보다 작은 값을 이동시키게 되면, swap 해줄 때 이미 비교한 값과 자리를 바꿔주게 된다.
그렇기 때문에 그때는 i++을 해주어 다음 값으로 v와 비교를 진행해야 한다.
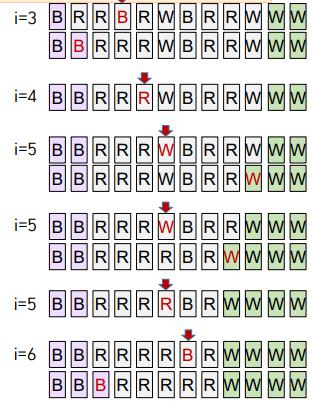
def partition3Way(a, lo, hi):
if (hi <= lo):
return
v = a[lo]
lt,gt = lo,hi # Pointers to <v and >v sections
i = lo
while i <= gt:
if a[i] < v:
a[lt], a[i] = a[i], a[lt] # Swap
lt, i = lt+1, i+1
elif a[i] > v:
a[gt], a[i] = a[i], a[gt] # Swap
gt = gt-1
else: i = i+1
print(a)
partition3Way(a, lo, lt-1)
partition3Way(a, gt+1, hi)
3-Way Quick Sort 성능
N개 원소 중 n개 서로 다른 key가 있고 i번째 key가 xi개 존재한다면 다음과 같은 횟수의 작업 필요하다.
ex. x1이 5개, x2가 6개, x3가 7개, 총 N이 18개면
-5 * log(5 / 18) -6 * log(6 / 18) -7 * log(7 / 18)이 된다.
모든 key가 다 다르면 (N개 key가 한 번씩 나오는 경우) : ~NlogN
n개 key가 N/n번씩 나온다면 : ~Nlogn
따라서 n이 작아질수록 (duplicate key가 많을수록) ~N에 가까워진다.
정리: Merge Sort, Quick Sort, 개선점, Applications
| Merge Sort | Quick Sort | 3-way Quick Sort | ??? | |
| 방법 | 작은 조각 -> 큰조각 순으로 merge 하면서 정렬 | 큰 조각 -> 작은 조각 순으로 partition 하면서 정렬 | 3조각으로 분할 후 왼쪽, 오른쪽 조각만 이어서 분할 | |
| Best | NlogN | NlogN | N | N |
| Average | NlogN | NlogN | NlogN | NlogN |
| Worst | NlogN | N^2 / 2 | N^2 / 2 | NlogN |
| 추가 공간 필요? | ~N 추가 공간 필요 | 불필요 | 불필요 | 불필요 |
| Stable | Yes | No | No | Yes |
'컴퓨터공학 > 알고리즘2' 카테고리의 다른 글
| [알고리즘2] Priority Queue (0) | 2022.10.21 |
|---|---|
| [알고리즘2] Collinear Point 구현 - 실습 (0) | 2022.10.21 |
| [알고리즘2] Convex Hull 구현 with Sorting - 실습 (0) | 2022.10.13 |
| [알고리즘2] Sorting (Shell Sort, Shuffle Sort, Convex Hull) (0) | 2022.10.13 |
| [알고리즘2] Percolation with Union Find(WQU) - 실습 (0) | 2022.10.11 |