[수치해석] Ch4_1. Truncation Errors and the Tayor Series

복습하기 위해 학부 수업 내용을 필기한 내용입니다.
이해를 제대로 하지 못하고 정리한 경우 틀린 내용이 있을 수 있습니다.
그러한 부분에 대해서는 알려주시면 정말 감사하겠습니다.

▶Truncation Errors

Truncation Error는 정확한 수학적 절차 대신 근사치를 사용하여 발생하는 오류이다.

728x90

▶The Taylor Series

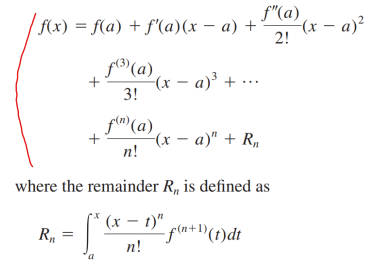
• 함수 값과 다른 점에서의 파생물 측면에서 한 점에서 함수 값을 예측하는 수단을 제공한다.
  • 한 점을 추정(근사)할 때, 다른 지점의 미분 값으로 그 값을 추정할 수 있다.
• 모든 smooth 함수가 다항식으로 근사될 수 있다.

zero-order approximation

first-order approximation

식은 직선 형태로 되어 있으며, xi와 xi+1 사이의 함수의 증가 또는 감소를 예측할 수 있다.

second-order approximation

the complete Taylor series expansion

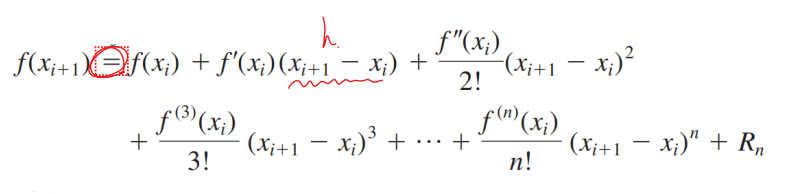
n을 크게 하면 할수록 오차가 줄어든다.

xi와 xi+1 사이의 간격이 작으면 작을수록 오차가 줄어든다.

오차는 (n +1)번째 거듭제곱으로 상승된 단계 크기 h에 비례한다. 
오류가 O(h) 인 경우 스텝 크기를 절반으로 줄이면 오류가 절반으로 줄어든다. 
반면에 오차가 O(h2)인 경우 스텝 크기를 반으로 줄이면 오류가 1/4이 된다.